




How to Find All Factors of 85 with Simple Methods
A factor is a number that completely divides the original number. Real numbers that can evenly divide the number 85 are factors of $85$. There is no residue if $"x"$ is the factor of $85$, since $"x"$ divides $85$ into equal parts. For instance, $12$ divided by $3$ is $4$, then 3 is a factor of $12$. Consequently, $3$ divides $12$ into four equal parts, leaving $0$ as the remainder. Since $85$ can only be divided by $1, 5, 17 and 85$. Therefore these are factors of 85.
Let's use straightforward methods in this article to determine the factors, pair factors, and prime factors of $85$.
What is the Factor of $85$?
The natural numbers that can divide a number 85 evenly are factors of $85$.These factors divide the original number into equal numbers of parts. For example, $85$ is divisible by $5$ (by the divisibility rule). So, $85$ divided by $5$ is equal to $17$. Hence, $5$ divides the $85$ into $17$ equal parts.
We can determine the other factors of $85$ with the help of the division method. $85$ has more than two factors, thus, it is a Composite number.

Factor of 85
How to Find Factors of $85$?
The natural numbers that can divide a number 85 evenly are factors of $85$. So the way you find and list all of the factors of $85$ is to go through every number up to and including $85$ and check which numbers result in an even quotient.
When the product of two natural numbers results in $85$, then the two numbers are the factors. We already know that $1$ is the factor of all the natural numbers and also, the original number is the factor of itself.
$85 \div 1 = 85$
$85 \div 2 = 42.5$ So, 2 is not a factor of 85.
$85 \div 5 = 17$
$85 \div 17 = 5$
$85 \div 85 = 1$
Therefore, the factors of $85$ are $1, 5, 17 and 85$.
Prime Factorisation of $85$
Prime factorization is the process of finding the prime terms or prime factors which, when multiplied, give the original number. So for performing prime factorization we divide the original number with prime numbers, which can divide by it, and then stop the process only when a result is a prime number.
Considering the prime numbers for the division process, we know that $85$ is divisible by $5$:
$\Rightarrow 85 \div 5 =17$
Since $17$ is a whole number and a prime number the next step would be as follows.
$\Rightarrow 17 \div 17 =1$
Therefore the answer would be: $85 = 5 \times 17$ since both $5$ and $17$ are prime numbers.
So the prime factorization of $85$ can be written as
$85 = 5 \times 17$.
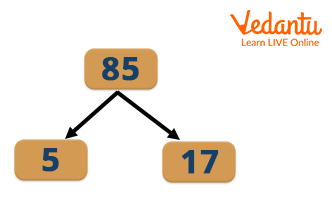
Pair Factors of 85
A factor pair is a pair of numbers that, when multiplied, will result in the original number (or the same product). To calculate the factor pair, factors are frequently presented as pairs of numbers. They are referred to as factor pairs. For example- factor pairs of $6$ include, $\left ( 1,6 \right )$ and $\left ( 2,3 \right )$.
Factor Pairs of $85$ are combinations of two factors that, when multiplied together, equal $85$. Here are all the Positive Factors Pairs of $85$.
$1 \times 85 = 85$
$5 \times 17 = 85$
$17 \times 5 = 85$
$85 \times 1 = 85$
Like we said above, Factors of $85$ include negative numbers as well. Minus times minus equals plus, thus, you can convert the Positive Factor Pair list above by simply putting a minus in front of every factor to get all the Negative Factor Pairs of $85$.
$\left ( -1 \right ) \times \left ( -85 \right ) = 85$
$\left ( -5 \right ) \times \left ( -17 \right ) = 85$
$\left ( -17 \right ) \times \left ( -5 \right ) = 85$
$\left ( -85 \right ) \times \left ( -1 \right ) = 85$.
Prime Factors of $85$
A number can be expressed as the product of its prime factors through the process of prime factorization. A number with exactly two factors, $1$ and the number itself, is said to be a prime number. As an illustration, let's use the number $30$. Even though we are aware that $30 = 5\times 6$ and $6$ is not a prime number.
We are aware that the number $85$ is a composite number, which implies its factors are $1, 5, 17 and 85$. As a result, $5$ and $17$ are the only prime factors.
Common Factor of $85$ and $25$
Common factors are those that are shared by two or more different numbers. To put it another way, a common factor is a number dividing a group of two or more numbers exactly. List each of the factors of the two integers separately to determine the common factors between them. Now list the elements that both numbers have in common. These elements are referred to as the provided two numbers' common components.
Let’s take an example to find common factors of $85$ and $25$.
Knowing that $1, 5, 17 and 85$ are the factors of $85$. $25$'s factors are $1, 5, and 25$.
Consequently, $1$ and $5$ are the common factors of $85$ and $25$.
Solved Examples
Example 1: What are the factors of $85$?
Solution: The natural numbers that can divide a number(85) evenly are factors of $85$. As a result, the factors of the number $85$ are $1, 5, 17 and \;85$. If we divide $85$ by any negative of these integers, then the resulting number will always be a factor of 85. Generally, we consider only positive numbers as factors.
Example 2: Can you assist Avinash with adding up all the factors of $85$?
Solution: First, we have to take out the factors of $85$.
$85 = 1, 5, 17, 85$
Here we can see that the factors of $85$ are $1, 5, 17 and 85$.
We can conclude here that If you add up all the components of $85$,
you get $1 + 5 + 17 + 85 = 108$
Example 3: Ryan's teacher told him that $\left ( -5 \right )$ is one of the factors of $85$. Can you help him find the other factor?
Solution: Since, $\left ( -5 \right )$ is one the factor of $85$, we will divide $85$ by $\left ( -5 \right )$ to get the other factor.
The other factor is $85 \div \left ( -5 \right ) = -17$
Hence, $-17$ is the other factor.
Conclusion
The number $85$ is an odd and composite number in mathematics. The only numbers with more than two elements are composite numbers. Each of the factors are either less than or equal to the original number. A given integer has a finite number of factors. Factors of $85$ are numbers that leave no residue when divided by $1, 5, 17 and 85$. This was a brief overview of factors of $85$ to help you become familiar with factorization.
Practise Problems
1. Determine the product of factors of 85.
2. Evaluate the LCM of 85 and 51.
Answers
1. 7225
2. 255
List of Related Articles
FAQs on Factors of 85 Explained for Students
1. Is the number $85$ prime? How do you tell whether $85$ is a composite or prime number?
The number $85$ is not prime. 85 can be divided by $1, 5, 17$, and $85$. A number must have exactly two factors to be recognised as a prime number. $85$ is not a prime number because it has more than two factors, including $1, 5, 17$, and 85$. Yes, considering that $85$ has more than two factors, including $1, 5, 17$, and $85$. In other words, the fact that 85 has more than two factors helps make it a composite number.
2. What are the common factors of $51$ and $85$?
A whole number of a factor of two or more numbers is referred to as a common factor. To determine the common factors of $51$ and $85$, follow the steps below:
Step 1: List the factors of each integer that is given.
$1, 5, 17$, and $85$ make up the number $85$.
$1, 3, 17$ and 51 make up the number $51$.
Step 2: Identify the shared factors among the given numbers and list them.
1 and 17 are hence the common factors.
3. Find the first 10 multiples of the number $85$.
The results of multiplying 85 by an integer are multiples of 85. Therefore,
$85 \times 1 = 85$
$85 \times 2 = 170$
$85 \times 3 = 255$
$85 \times 4 = 340$
$85 \times 5 = 425$
$85 \times 6 = 510$
$85 \times 7 = 595$
$85 \times 8 = 680$
$85 \times 9 = 765$
$85 \times 10 = 850$
Hence, $85, 170, 255, 340, 425, 510, 595, 680, 765, and 850 are the first 10 multiples of 85$.











