Factors of 128 Explained With Easy Steps and Examples

Factors of a number are defined as the integers that completely and evenly divide the given number without leaving any remainder. We can write a given number into a product of its factors. This is known as the factorization of a number. The factors are the numbers that are always smaller than or equal to the given number and divide the number without leaving a remainder.

What is a Factor?

A factor of a number is a number other than a given number that divides the given number without leaving any remainder. It means we can multiply finite copies of a factor together to get the original number. For example, 2 is divisible by both 1 and 2. So, the factors of 2 are 1 and 2.

How to Find Factors of 128?

The given number is 128, we know there are at least two factors of the number 1 and the number itself. So, two of the factors of 128 are 1 and 128. To find the remaining factors, we divide 128 by 2, 3, 4,… till 127 (as the factors are always less than 128). We know that 128 is divisible by 2, the remainder is zero and we get the quotient 64. So, 2 and 64 are the factors of 128. Next, we need to check upto 64 only. After 2, we find that 4 divides 128 exactly with the quotient of 32. So, 4 and 32 are also the factors of 128. Next, we get 8 and 16 as factors of 128 and no other number divides 128 exactly. Hence, we get the factors of 128 as 1, 2, 4, 8, 16, 32, 64, and 128.

If we consider 128 as an integer, then the factors of 128 will include both positive and negative factors as 1, -1, 2, -2, 4, -4, 8, -8, 16, -16, 32, -32, 64, -64, 128, and -128.

Prime Factors of 128

Prime numbers are the numbers having only two factors, i.e., 1 and the number itself. The factors of 128 are 1, 2, 4, 8, 16, 32, 64, and 128. Here, the only prime is 2. Therefore, 2 is the only prime factor of 128.

Prime Factorization of 128

In order to find the prime factorization of 128, find the prime factors of 128. Recall that Prime Factors are the numbers that have only two factors 1 and the number itself. From the factors of 128, the prime number is 2 only.

So, the prime factor of 128 is 2.

Now, we see that $2^7=128$ and 2 is a prime number. So, Prime Factorization of 128 is

$2\times2\times2\times2\times2\times2\times2$.

We can do this in another way:

Start from 2(prime number). Is 128÷2? YES.

Write 2 to the left of 128 and 128÷2, i.e., 64 below 128.

Next, do it for 64. Continue till we get 1 at the end.

Prime Factorization of 128

Now, write the numbers in the left column in the form of multiplication as $128=2\times2\times2\times2\times2\times2\times2$.

This is the prime factorization of 128.

This can also be written as $128=2^7$ (Exponential Form).

If we consider 128 as an integer, then we can write the prime factorization of 128 as $(-2)^6 \times 2 $ or $ -(-2)^7$. Other factorizations are possible in this case.

Prime Factorization of 128 Using Factor Tree

Factor trees are a way of expressing the factorization of a number in terms of its prime factors. It uses repeated division by prime numbers to get the prime factorization.

All the branches of the tree are split into factors. When the factors at the end are prime numbers, we stop and the numbers at the end are prime factors. Writing them in multiplicative form gives a prime factorization of 128 using a factor tree.

We start dividing the number by prime numbers and write the number and the quotient as the branches of the tree. This process is repeated till we get all the prime numbers at the end.

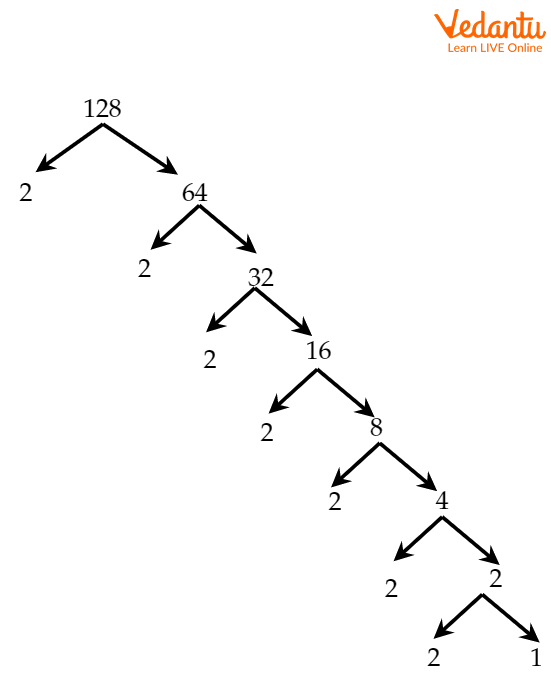
Factor Tree of 128

Here, the last row contains 2’s only (prime numbers).

So, the prime factorization of 128 is $2\times2\times2\times2\times2\times2\times2$.

Factors of 128 in Pairs

To write all the factors of 128 in pairs, we see that

$1\times128=128$

$2\times64=128$

$4\times32=128$

$8\times16=128$

$-1\times (-128)=128$

$-2\times (-64)=128$

$-4\times(-32)=128$

$-8\times (-16)=128$

So, writing the numbers on the left-hand side in pairs, we get (1,128), (2,64), (4,32), (8,16), (-1,-128), (-2,-64), (-4,-32), (-8,-16) and these are the factors of 128 in pairs.

Number of Factors of 128

If the prime factorization of N is in form \[N{\rm{ }} = {X^a}{y^b}{z^c}\], then the number of positive factors is \[\left( {a + 1} \right)\left( {b + 1} \right)\left( {c + 1} \right)\].

The prime factorization form of 128 is \[{2^7}\].

The number of positive factors of 128 is \[7 + 1 = 8\].

The number of negative factors in a number is the same as the number of positive factors in a number.

The total number of factors of 128 is 8+8 =16.

Solved Problem

1. What is the sum of all positive factors of 128?

Solution:

The factors of 128 are 1, 2, 4, 8, 16, 32, 64, and 128.

The sum of the factors is 1+2+4+8+16+32+64+128 = 255

2. Find the prime factors of 45.

Solution:

Prime Factorization 45

The prime factorization form of 45 is $3\times 3\times 5$.

Thus, the prime factors of 45 are 3 and 5.

Practice Questions

1. Find the prime factors of 65.

Answer: The prime factors are 5 and 13.

2. What is the prime factorization of 28?

Answer: The prime factorization of 28 is \[2^{2}\times 7\].

Key Features

• To find the factors of 128, we can use a factor tree.

• The factors of 128 are 1, 2, 4, 8, 16, 32, 64, and 128 and their negative counterparts.

• The factor pairs of 128 are (1,128), (2,64), (4,32), (8,16), (-1,-128), (-2,-64), (-4,-32), and (-8,-16).

Interesting Facts

• A composite number is never a prime number.

• If a number has more than two positive factors, it is a composite number.