Speed Distance Time Word Problems with Solutions

Speed, distance, and time are the three main pillars behind mathematics and physics. Whenever you are presented with a question related to any kind of transportation, you should immediately relate to these concepts. The train speed, the relation between the time taken by two cars at different speeds or even a simple question about a person walking from one place to another can be answered using simple formulas.

What is Speed?

When you think of speed, you must think of how fast? Speed is all about calculating the rate at which something can be accomplished.

A Device Used to Measure Speed Known as a ‘Speedometer’

What is Distance?

Distance in this concept refers to the distance travelled. It means how far? It can be measured in meters, for small distances and kilometres, for larger distances.

Distance is the Measurement From One Place to Another

What is Time?

Time is the answer to the question, how long? The best way to measure time is using the ‘world clock.’ In ancient times, time was measured with the help of the sun and the moon, and other celestial objects.

Time as Shown by a Clock

Relation Between Speed Distance and Time

There is a very simple mathematical relation between speed, distance and time.

$\text{speed=}\frac{\text{distance}}{\text{time}}$

$\text{time=}\frac{\text{distance}}{\text{speed}}$

$\text{distance=speed }\!\!\times\!\!\text{ time}$

These relations can be memorised using the triangle method. See the following image to understand the use of this method.

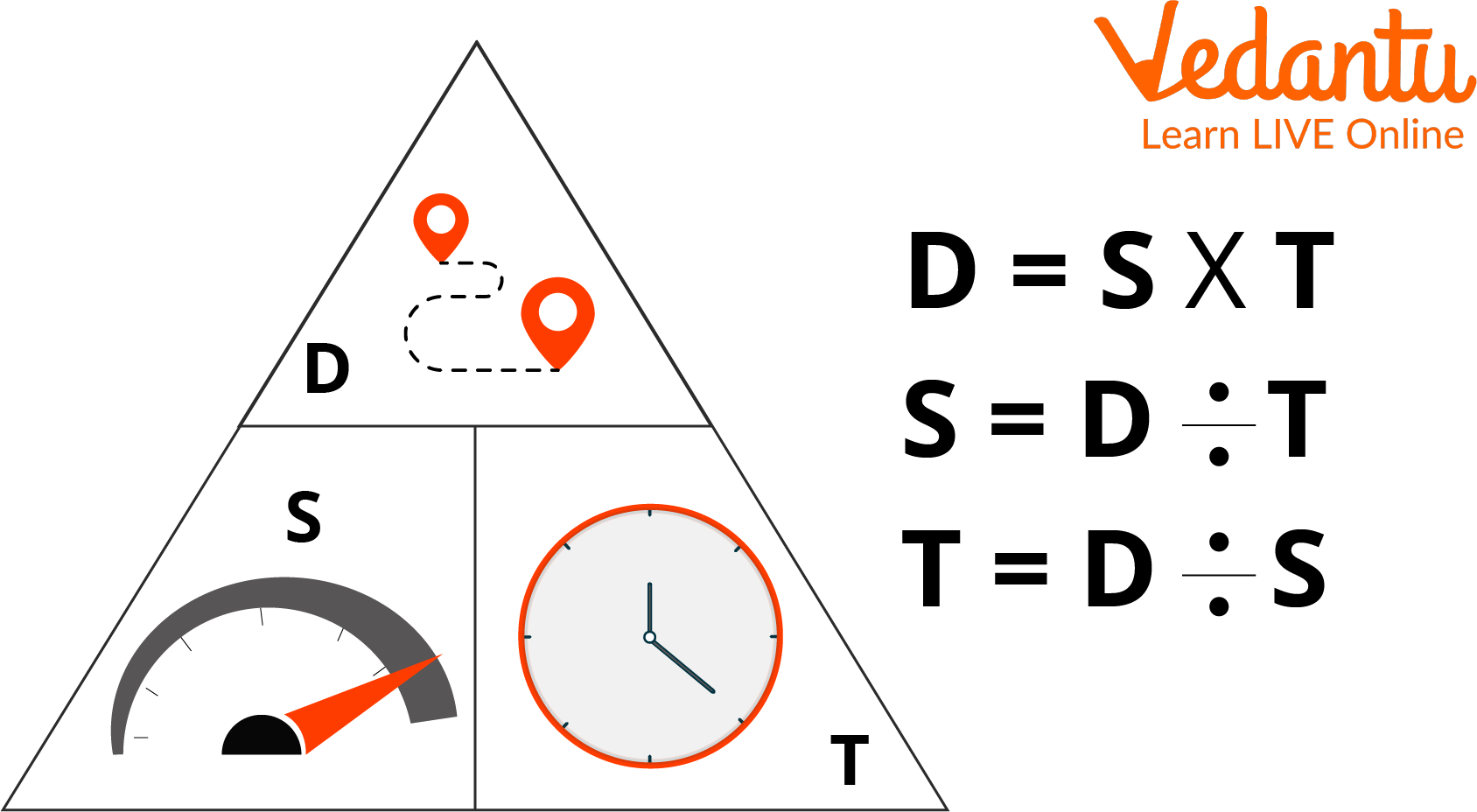
Explaining the Triangle Method

Speed Distance Time Word Problems With Solutions

Q1. A train is travelling at a speed of 160 km/hour. It takes 15 hours to cover the distance from city A to city B. Find the distance between the two cities.

Solution:

Speed= 160 km/hr

Time= 15 hours

Using the formula, $\text{distance=speed }\!\!\times\!\!\text{ time}$

Distance= $160\times 15=2400km$

Answer: The distance between city A and city B is 2400km

Q2. A car travelling from city A to city C completes the journey in 3 hours, whereas a person travelling on a bike completes the journey in 5 hours. What is the speed of the man on the bike if the car is travelling at 45 kmph?

Solution:

Find the distance using the information on the car

Using the formula, $\text{distance=speed }\!\!\times\!\!\text{ time}$

Speed= 45km/hour

Time= 3 hours

$\therefore \text{distance}=45\times 3=135km$

Using the distance, we can find the speed of the bike

Formula used, $\text{speed=}\frac{\text{distance}}{\text{time}}$

Time taken by bike is 5 hours

$\therefore \text{speed}=\frac{135}{5}=27$

Answer: The bike is moving at a speed of 27 kmph.

Q3. A person travels at a speed of 15 kmph from point A to point B, which are 25 km from each other. Another person is travelling from point C to point B, 44 km from each other. Both people start their journey at the same time; the second person arrives at the point 2 hours after the first. What is the speed at which the second person was travelling?

Solution:

Speed of person 1 = 15km/hour

Distance travelled by person 1= 25 km/hour

Time taken by first-person = $\frac{\text{distance}}{\text{speed}}=\frac{25}{15}=\frac{5}{3}$hours

Note: While solving the questions, keep the answers in fractions until you reach the final answer to make calculations easier.

Time taken by second person =$\frac{5}{3}+2=\frac{11}{3}$hours

Distance travelled by second person= 44 km

$\therefore \text{speed}=\frac{\text{distance}}{\text{time}}=\frac{44}{\frac{11}{3}}=\frac{44\times 3}{11}=4\times 3=12$kmph

Answer: The second person was travelling at a speed of 12kmph.

Q4. Raju is travelling from one station to another 560km away in a train which is moving at a speed of 125kmph. Monu is travelling to the same destination at a speed of 80kmph. Monu starts his journey 3 hours after Raju, from 120 km closer to the destination. How long will Raju have to wait at the train station for Monu to arrive?

Solution:

Distance travelled by Raju = 560km

Speed of Raju= 125km/hour

∴ Time taken by Raju to reach the station = $\frac{\text{distance}}{\text{speed}}=\frac{560}{125}=\frac{112}{25}$hours

Distance travelled by Monu = $560-120=440$km

The speed at which Monu travelled = 80kmph

Time taken by Monu to complete journey = $\frac{440}{80}=\frac{22}{4}=\frac{11}{2}$hours

Total time taken by Monu = $\frac{11}{2}+3=\frac{17}{2}$hours

Therefore, the time Raju had to wait = difference between the two times taken

$\therefore \frac{17}{2}-\frac{112}{25}=\frac{17\times 25}{50}-\frac{112\times 2}{50}=\frac{201}{50}=4.02$hours

Answer: Raju had to wait for 4.02 hours at the train station

Convert 4.02 hours to hours and minutes

$\therefore 0.02=\frac{2}{100}\times 60=1.2$minutes

$\therefore 0.2=\frac{2}{10}\times 60=12$seconds

Therefore, to be precise, Raju had to wait at the train station for 4 hours, 1 minute and 12 seconds.