




What Are the Factors and Prime Factors of 122?
In Mathematics, there are two types of numbers: prime and composite. The numbers with no factor other than 1 and the number itself are known as prime numbers. The numbers with at least one factor other than 1 are known as composite numbers. If a given number, when divided by some number, gives the whole number as a quotient and 0 as a remainder, then the divisor is the factor of the given number.
Factors of a Number
The factor of a given number is a value that divides the number completely, leaving 0 as the remainder. The factors of a number can be positive as well as negative. For example, if 2 and 3 divide 6 completely, then we can say that 2 and 3 are factors of 6.
Factorisation of a Number
Factorisation refers to writing a number as the product of different smaller numbers. The smaller numbers can be either prime numbers or composite numbers. The smaller numbers are referred to as the factor of the given number. For example, 3 and 27 are the factors of 81.
What are the Factors of 122?
Given the number is 122, it is known without a doubt that it will have at least two factors which are 1 and the number itself. So two of the factors are 1 and 122. Now to find the remaining factors of 122, we need to divide 122 by numbers starting from 2 to 121. The numbers which will give 0 as the remainder are the factors of 122. We find out that the numbers satisfying this condition are 2 and 61.
Further, no such number will divide 122 completely with 0 as the remainder. Hence, we get the factors of 122 as 1, 2, 61 and 122. Considering 122 as an integer, we can include both positive and negative numbers as the factors of 122. Thus, all the factors of 122 will be 1, -1, 2, -2, 61, -61, 122 and -122.
Prime Factors of 122
The numbers with 1 and themselves as factors are known as prime numbers. The factors of 122 are 1, 2, 61 and 122. Out of these, 2 and 61 are prime numbers. Thus, the prime factors of 122 are 2 and 61.
The prime factors of a number can also be represented in a factor tree. A factor tree is a diagram in which we find the factors of a number and then further break those numbers into smaller numbers until further factorisation is impossible. In the end, we get the prime factors of the original number.
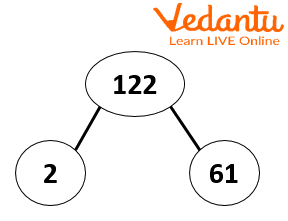
Factors tree of 122
Prime Factorisation of 122
Any composite number can be expressed as the product of primes. This process of representing 122 as a product of primes is known as prime factorisation. For prime factorisation of a number, we start dividing it with the smallest prime number, which will give 0 as the remainder. Next, we divide the quotient obtained with the next prime number to get the remainder as 0. This process is repeated till the quotient obtained is 1.
As we know that 122 is a composite number, so it will have prime numbers as its factors. So to express 122 as the product of primes, first, divide it by the smallest prime number; here, it is 2, such that the remainder is 0. It will give 61 as the quotient, that is, \[122 \div 2 = 61\].
Now, divide the quotient with the next smallest prime number such that the remainder is 0. Here we observe that 61 is itself a prime number. So the next prime number that divides 61 will be 61 itself, giving 1 as a quotient.
Thus, the prime factorisation of 122 is $2 \times 61.$
Factors of 122 in Pairs
The pair of numbers, when multiplied with each other, give 122 as products are the pair factors of 122.
As we know that \[1 \times 122 = 122\]. So, (1, 122) is a pair factor. Also \[2 \times 61 = 122\]. So, (2, 61) is a pair factor.
Considering 122 as an integer, \[\left( { - 1} \right) \times \left( { - 122} \right) = 122\] and \[\left( { - 2} \right) \times \left( { - 61} \right) = 122\]. So, (-1, -122) and (-2, -61) are also pair factors.
Number of Factors of 122
The factors of the number 122 are 1,2,61 and 122. The negative value of the factors is also a factor of 122, which are -1,-2,-61, and -122. The total number of factors of 122 are 8.
Interesting Facts
2 is the only even prime number.
1 is neither prime nor composite.
The prime numbers that are two spaces apart are called twin primes.
Products of two prime numbers are known as semiprime numbers.
Solved Examples
Q1. What is the sum of all the prime factors of 122?
Ans: The prime factor of 122 is \[2 \times 61\]. The Sum of all the prime factors is 2+61=63.
Q2. Find the common prime factors of 122 and 76.
Ans: Prime factorisation of \[122 = 2 \times 61\]
Prime factorisation of \[76 = 2 \times 2 \times 19\]
From above, we can see that the common prime factor of 122 and 76 is 2.
Q3. Which of the following is not a prime factorization?
\[25 = 5 \times 5\]
\[64 = 8 \times 4 \times 2\]
\[120 = {2^3} \times 15\]
Ans: In (a) 25 is written as the product of two 5s. As 5 is a prime number, thus 25 has been expressed as the product of primes.
In (b) 64 is written as the product of 8, 4 and 2. 2 is a prime number, but 8 and 4 are not prime numbers; they can be further expressed as smaller prime numbers as 8 = 23 and 4 = 22. Thus, 64 has not been expressed as the product of primes.
In (c), 120 is written as the product of 23 and 15. 2 is a prime number, but 15 is not a prime number; it can be expressed as \[3 \times 5\]. Thus, 120 has not been expressed as the product of primes.
Practice Questions
Q1. Which of the following is not a prime factorisation?
a. \[27 = 1 \times 27\]
b. \[100 = 2 \times 2 \times 5 \times 5\]
c. \[100 = {2^2} \times {5^2}\]
Ans. a. \[27 = 1 \times 27\]
Q2. What is the sum of all the positive factors of 122?
Ans. 186.
Key Features
Factorisation refers to breaking a given number into smaller numbers such that the product provides the original number.
We can also perform prime factorisation of a number, expressing a number as a product of primes.
The prime factorisation of 122 is \[2 \times 61\].
Given number 122 is a composite number with 1, 2, 61 and 122 as the positive factors and -1, -2, -61 and -122 as negative factors.
List of Related Articles
FAQs on Factors of 122 Explained with Examples
1. What are all the factors of 122?
The factors of a number are integers that divide it without leaving a remainder. To find the factors of 122, we look for all the numbers that can divide 122 evenly. The factors of 122 are 1, 2, 61, and 122. Each of these numbers divides 122 perfectly.
2. What is the prime factorisation of 122?
The prime factorisation of a number is the process of expressing it as a product of its prime factors. For 122, we start by dividing it by the smallest prime number, which is 2. The result is 61. Since 61 is itself a prime number, the process stops. Therefore, the prime factorisation of 122 is represented as the product 2 × 61.
3. How do you find the factor pairs for the number 122?
Factor pairs are pairs of numbers that, when multiplied together, result in the original number. To find the factor pairs of 122, we can systematically check which numbers multiply to give 122. The factor pairs are:
- 1 × 122 = 122
- 2 × 61 = 122
Thus, the factor pairs of 122 are (1, 122) and (2, 61).
4. How can you use the factor tree method to determine the prime factors of 122?
The factor tree method is a visual technique for finding prime factors. Here is the step-by-step process for 122:
- Start with the number 122 at the top of the tree.
- Draw two branches down to a pair of factors, such as 2 and 61.
- Examine each factor. The number 2 is a prime number, so we circle it and that branch ends.
- Next, examine the number 61. Since 61 is also a prime number, we circle it as well.
The process concludes when all branches end in a circled prime number. The prime factors are the circled numbers: 2 and 61.
5. What is the difference between a simple factor and a prime factor, using 122 as an example?
The key difference lies in their own properties. A simple factor is any number that divides another number evenly. For 122, the complete list of factors is 1, 2, 61, and 122. In contrast, a prime factor is a factor that is also a prime number (a number greater than 1 that only has two factors: 1 and itself). For 122, the prime factors are only 2 and 61, because 1 is not a prime number and 122 is not a prime number.
6. Based on its factors, how can you determine if 122 is a prime or a composite number?
A number's classification as prime or composite depends on its total number of factors. A prime number has exactly two distinct factors: 1 and itself. A composite number has more than two factors. Since the number 122 has four factors (1, 2, 61, and 122), it has more than two factors. Therefore, 122 is a composite number.
7. Why is understanding prime factorisation important for solving more complex Maths problems?
Understanding prime factorisation is a fundamental skill in mathematics that is essential for many advanced concepts, as per the CBSE syllabus. It is the core method used for:
- Finding the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of numbers.
- Simplifying fractions to their lowest terms.
- Calculating square roots and cube roots.
- Solving problems in number theory and algebra.
It allows us to break down complex numbers into their basic building blocks, which simplifies calculations and problem-solving.

















