Factors of 112

Factors of a number are the integers that divide the number evenly, without leaving a remainder. Factors of 112 are 1, 2, 4, 7, 8, 14, 16, 28, 56, 112 and the negative counterparts of these numbers i.e. −1, −2, −4, −7, −8, −14, −16, −28, −56, and −112.

Factors can be both Prime and Composite; prime factors of a number can be found using a factor tree.

What are the factors of 112?

Factors of 112 are the integers that divide 112 completely and evenly without leaving a remainder. 112 has 20 factors in total; all the factors of 112 are listed below

\[ \pm 1, \pm 2, \pm 4, \pm 7, \pm 8, \pm 14, \pm 16, \pm 28, \pm 56, and \pm 112 \]

The factors of 112 can be determined in a straightforward way,

To find all the positive factors of 112, first, start with 1 and 112, since it is trivial that 1 and the number itself are always factors of a given number. Thus, it can be said that 112 has at least 2 factors 1 and 112.

\[112 = 1 \times 112\]

It is clear that 112 is also divisible by 2 since it is an even number; thus, a factor of 2 can be moved from 112 to 1 so that this expression looks like,

\[112 = 2 \times 56\]

Similarly, a factor of 2 can be repeatedly moved from the right-side factor to the left-side factor until the right-side factor results in an odd number

\[112 = 4 \times 28\]

\[112 = 8 \times 14\]

\[112 = 16 \times 7\]

Here, the right-side factor is an odd number as well as a prime. Thus no more factors can be moved from the right-side to the left-side. Thus, the factors given by these expressions are the only distinct positive integers that divide 112, i.e. factors of 112.

It is also clear that in a similar manner, the negative factors of 112 can also be determined if the process started with -1 and -112.

Factors of 112 in Pairs

The list of all the factors of 112 in pairs is given by the iteration performed in the previous subheading.

The factors of 112 in pairs are pairs of numbers that, when multiplied together, result in 112. Thus, the factors of 112 in pairs are (1, 112), (2, 56), (4, 28), (7, 16), and (8, 14). When multiplied together, all of these pairs of numbers result in 112. There are also negative factors of 112 that can also be paired. The negative factors of 112 in pairs are (-1, -112), (-2, -56), (-4, -28), (-7, -16), (-8, -14).

The positive factors of 112 and the positive factors of 112 in pairs can be compared through the following table

And the negative factors of 112 and the negative factors of 112 in pairs can be compared through the following table

Prime Factors of 112

The factors of 112 can be classified into two categories, Prime and Composite. The prime factors of 112 cannot be further divided into factors other than 1 and the number itself, i.e., the factors of 112 that themselves have only 2 factors (1 and the factor itself) are the prime factors of 112. There are only two prime factors of 112 2 and 7.

Prime factorisation of 112 and Factor Tree of 112

By the fundamental principle of arithmetic, every number can be represented as a product of its prime factors, known as the prime factorisation of a number, which is unique.

Thus, it can be said that 112 can also be written as a product of prime factors 112, 2, and 7.

The prime factorisation of 112 can be done with the help of the factor tree of 112.

The factor tree can be represented in different ways. The 2 most common ways to represent a factor tree are given below as the factor tree of 112.

1. Simple table

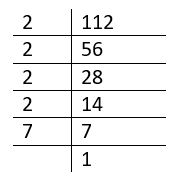
Table

In this factor tree of 112 the left column is the column of Prime factors of 112, and each prime factor divides the corresponding factor of 112 on the right column with the quotient of this division written on the right column in the next row.

2. Splitting Branches

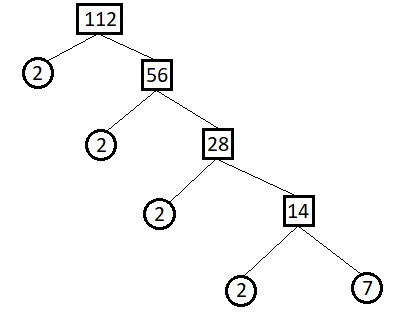
Factor tree of 112

In this factor tree of 112 the numbers written inside the circle are the prime factors and each line represents the factorisation of the number written in the box into two factors, similar to the tabular factor tree of 112 the numbers in the circle divide the number in the box connected to them and the quotient is connected by another line going right-side.

The prime factorisation of 112 given by the factor tree of 112 is,

\[112 = 2 \times 2 \times 2 \times 2 \times 7 = {2^4} \times 7\]

Problems:

1. What are the prime factors of 112?

Solution: We know that,\[112 = 2 \times 2 \times 2 \times 2 \times 7 = {2^4} \times 7\]

The factors of 112 are 2,4,7,8,14,16,28,56,112.

The prime numbers are 2, 7 among 2,4,7,8,14,16,28,56,112.

Thus the prime factors of 112 are 2 and 7.

Conclusion

This article discussed factors of 112 and the prime factorisation of 112. Factors of 112 are the numbers that divide 112 completely and evenly without leaving a remainder. There are 20 factors of 112, 10 of them are positive and 10 are negative. The factors of 112 are \[ \pm 1, \pm 2, \pm 4, \pm 7, \pm 8, \pm 14, \pm 16, \pm 28, \pm 56, and \pm 112 \]. These factors of 112 can also be paired such that they multiply to give 112 the factors of 112 in pairs are (1, 112), (2, 56), (4, 28), (7, 16), (8, 14), (-1, -112), (-2, -56), (-4, -28), (-7, -16), and (-8, -14). The factors of 112 that are prime are known as prime factors of 112, they are 2 and 7. The prime factorisation of 112 by factor tree is \[2 \times 2 \times 2 \times 2 \times 7 = {2^4} \times 7\].

Practice problem:

1. Find out the prime factors of the number 99.

2. Make a tree for factor 72.

List of Related Articles

• Factors of a number

• Prime factorisation

• Prime Factors