




Area and Perimeter Formulas Explained with Examples
Understanding the Difference Between Area And Perimeter is fundamental in geometry, especially for board exams and JEE. Recognizing how area and perimeter compare sharpens mathematical reasoning and problem-solving, ensuring accurate calculations in questions involving two-dimensional shapes and measurement-based scenarios.
Understanding Area in Mathematics
Area describes the amount of two-dimensional space taken up by a closed shape. It quantifies the region enclosed within the boundaries of a geometric figure and is expressed in square units.
For regular shapes, the area depends on specific formulae derived from their dimensions, making it essential for comparing properties of rectangles, triangles, or circles.
$A = l \times w$
Mathematical Meaning of Perimeter
Perimeter refers to the total length of the boundary or outline of a closed figure. This measurement is always one-dimensional and is reported in linear units.
Perimeter calculation involves summing the lengths of all sides of a given shape. Practical tasks like fencing a park or framing a picture rely on the correct determination of perimeter. The Difference Between Area And Perimeter clarifies their distinct roles.
$P = 2(l + w)$
How Area and Perimeter Differ: A Comparative Table
| Area | Perimeter |
|---|---|
| Space enclosed within a shape | Length around a shape’s boundary |
| Measured in square units (e.g., cm², m²) | Measured in linear units (e.g., cm, m) |
| Quantifies internal region | Quantifies total outline length |
| Two-dimensional attribute | One-dimensional attribute |
| Does not depend only on boundary length | Direct sum of side lengths |
| Relevant for tasks like painting or tiling | Relevant for fencing or edging |
| Area of rectangle: length × width | Perimeter of rectangle: 2(length + width) |
| Area of square: side × side | Perimeter of square: 4 × side |
| Area of circle: π × radius² | Perimeter (circumference) of circle: 2π × radius |
| Area may change with shape orientation | Perimeter remains unchanged by orientation |
| Not possible for area to be negative | Perimeter is always a positive value |
| Used to estimate enclosed content | Used to estimate material around a shape |
| Unit: m², cm², etc. | Unit: m, cm, etc. |
| Physical meaning: coverage | Physical meaning: border or length |
| Formula varies by shape type | Formula: sum of side lengths for polygons |
| Helps in calculating field or region size | Helps in calculating fence or edge size |
| Area stays constant if boundary reused efficiently | Perimeter can change with same area figures |
| Essential for surface-related calculations | Essential for frame- or path-related calculations |
| Represents size of the surface | Represents size of the outline |
| Can compare regions with different perimeters | Can compare outlines with different areas |
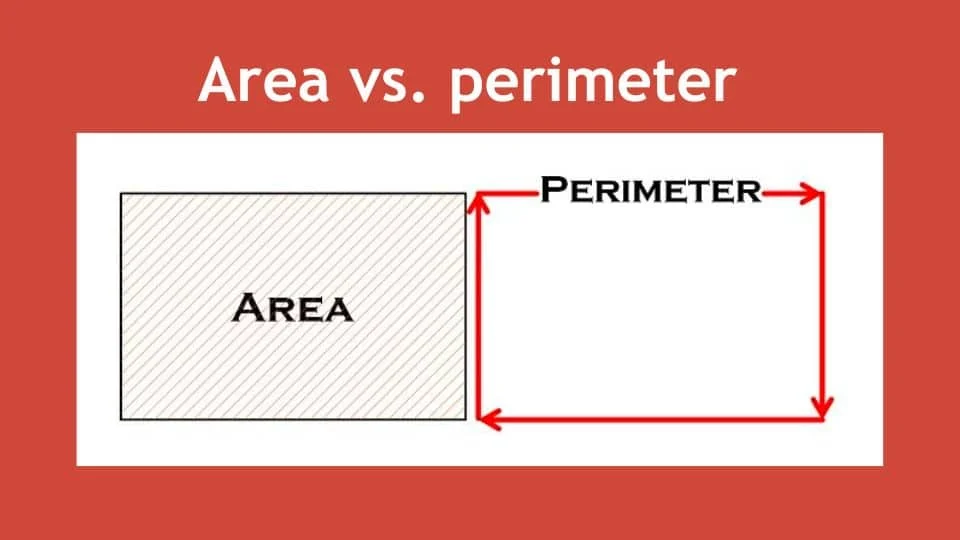
Core Distinctions Between Area and Perimeter
- Area measures surface, perimeter measures enclosing length
- Area expressed in square units, perimeter in linear units
- Area is two-dimensional, perimeter is one-dimensional
- Area focuses on region, perimeter focuses on boundary
- Area and perimeter can vary independently for same shapes
Simple Numerical Examples
For a rectangle with length 8 cm and width 3 cm, the area is $8 \times 3 = 24$ cm² and the perimeter is $2(8+3) = 22$ cm.
A square with side 5 m has area $5 \times 5 = 25$ m² and perimeter $4 \times 5 = 20$ m. Refer to the Area Of Square Formula to review this calculation.
Applications in Mathematics and Daily Life
- Area used for estimating paint or tile required
- Perimeter applied for fence length or border decoration
- Area calculation essential in agriculture and land measurement
- Perimeter determines total distance run on tracks
- Area helps in resource allocation over surfaces
Summary in One Line
In simple words, area quantifies the space inside a shape, whereas perimeter measures the total length around the shape.
FAQs on What Is the Difference Between Area and Perimeter?
1. What is the difference between area and perimeter?
Area measures the amount of space inside a shape, while perimeter is the total distance around its boundary.
Key differences:
- Area is measured in square units (like cm² or m²).
- Perimeter is measured in linear units (like cm or m).
- Area answers "How much surface does a shape cover?"
- Perimeter answers "How long is the boundary of the shape?"
2. How do you find the area and perimeter of a rectangle?
To find the area and perimeter of a rectangle, use:
- Area = Length × Breadth (l × b), measured in square units.
- Perimeter = 2 × (Length + Breadth) or 2(l + b), measured in linear units.
These formulas help you quickly calculate how much space the rectangle covers and the total distance around it.
3. Why is area measured in square units and perimeter in linear units?
Area is measured in square units because it represents surface covered, while perimeter is measured in linear units since it represents length around a shape.
For example:
- Area (like cm², m²) counts how many squares fit inside a shape.
- Perimeter (like cm, m) adds up the side lengths to measure boundary distance.
4. What are some real-life examples of area and perimeter?
In everyday life, area and perimeter help us calculate space usage and boundaries:
- Area: Covering floors with tiles, calculating farmland size, or painting walls.
- Perimeter: Fencing a garden, framing a picture, or putting borders around a playground.
5. Can two shapes have the same perimeter but different areas?
Yes, two shapes can have the same perimeter but different areas.
Example:
- A 6×2 rectangle and a 4×4 square can have the same perimeter (16 units) but different areas.
- This shows perimeter and area are related but not always equal for different shapes.
6. How do you find the perimeter of irregular shapes?
To find the perimeter of irregular shapes, add the lengths of all sides.
Steps:
- Measure each side of the shape carefully.
- Add all side lengths to get the total perimeter.
This method works for polygons and irregular figures where sides are not equal.
7. What is the formula for area and perimeter of a square?
For a square:
- Area = Side × Side (side²), measured in square units.
- Perimeter = 4 × Side, measured in linear units.
Use these formulas when all four sides of the shape are equal in length.
8. Why do we need to know the area and perimeter in mathematics?
Knowing area and perimeter helps us solve real-world problems involving space and boundaries.
- Area is important in construction, agriculture, and interior design.
- Perimeter helps measure fencing, borders, and frames.
Understanding both concepts is key for practical problem-solving and exams.
9. How is area different from surface area?
Area measures surface inside a two-dimensional shape, while surface area measures total area covering a three-dimensional object.
- Area: Applies to 2D shapes like rectangles and circles.
- Surface area: Applies to 3D solids like cubes, cuboids, and spheres.
10. Which is greater: area or perimeter?
Area and perimeter cannot be directly compared because they have different units and meanings.
- Area: Measures surface (square units).
- Perimeter: Measures boundary length (linear units).
Their values depend on the shape and its dimensions.
























