Formula derivation and solved examples of a minus b whole cube
Anything raised to the power 3 is known as a cube in arithmetic and algebraic terms which means to cube a number just multiply its three times.The cube of any number is denoted by superscript 3.The cube number is when a number is multiplied by twice itself.
A binomial is multiplied by itself three times to form the cube of a binomial.Thus we can say that the cube of any number ‘a ‘ can expressed as \[a \times a \times a\] or \[{a^3}\] is known as cube number. This binomial is an algebra expression consisting of two terms i.e., a+b or a-b and its cube can be expressed as \[(a - b) \times (a - b) \times (a - b)\] or
\[{(a - b)^3}\].
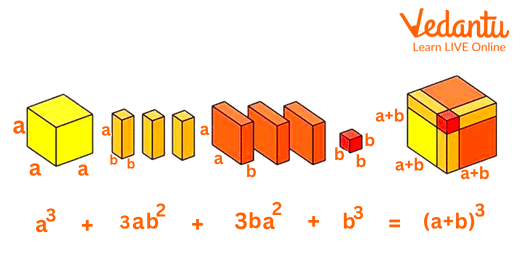
Cube of Binomial
Cube of The Difference of Two Binomials
The basic formula for the cube of difference of two binomial \[{(a - b)^3}\]is which can be expanded as follow:
\[\begin{array}{l}{(a - b)^3} = (a - b)(a - b)(a - b)\\\ = ({a^2} - 2ab + {b^2})(a - b)\\\ = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\\ = {a^3} - 3ab(a - b) - {b^3}\end{array}\]
We can summarize the cube of a binomial with a subtraction sign in between can be expressed as \[{(a - b)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\] .
Example: \[{(x - 4)^3}\]
Solution: \[{(x - 4)^3} = {x^3} - 3{x^2}4 + {\kern 1pt} 3x{4^2} - {4^3}\]
\[{(x - 4)^3} = {x^3} - 12{x^2} + 48{x} - {64}\]
Cube of Difference
Without actually computing the cubes, the difference of cubes formula is used to determine the difference of cubes between two numbers. The cube binomials are factorized using the difference of cubes formula. The cube of the difference between two expressions is equal to the cube of the first, minus three times the product of the squares of the first and second, plus three times the product of the first and second squares of the first and second, minus the cube of the second.
Formula:\[{a^3} - {b^3} = (a - b)({a^2} + ab + {b^2})\]
Cube of Difference Examples
The following are examples of the cube of differences i.e.,
Solve it
a) \[({x^3} - 125)\]
Solution:\[ \Rightarrow {x^3} - {5^3} = (x - 5)({x^2} + 5x + 25)\]
b) Factorize the expression\[(8{x^3} - 125)\] by using the difference of cubes formula.
Solution:We can write the given expression as \[8{x^3} - 125 = {(2x)^3} - {5^3}\]
Substituting the values a=2x and b= 5 in the formula of the difference of cube\[ = (2x - 5)({(2x)^2} + (2x) \times 5 + {(5)^2})\]
\[= (2x - 5)(4{x^2} + 10x + 25)\]
The Cube of the Difference of 1 and A Variable
The cube of difference of 1 and a variable can be expressed as \[(1 - {x^3})\] where a=1 and b=x and then we solve it in the same way using the cube of difference formula.
For example:\[\begin{array}{l}(1 - 125{x^3}) = (1){}^3 - {(5x)^3}\\ \Rightarrow (1 - 5x)(1 + 5x + 25{x^2})\end{array}\]
Solved Questions
1.Expand it: \[{(4x - 3y)^3}\]
Ans: \[\begin{array}{l} \Rightarrow {(4x)^3} - 3{(4x)^2}(3y) + 3(4x){(3y)^2} - {(3y)^3}\\ \Rightarrow 64{x^3} - 144{x^2}y + 108x{y^2} - 27{y^3}\end{array}\]
2.Factorise: \[(1 - 64{x^3}{y^3})\]
Here, a=1 and b=4xy
Ans:\[\begin{array}{l} \Rightarrow {(1)^3} - {(4xy)^3}\\ \Rightarrow (1 - 4xy)[({(1)^2} + (1)(4xy) + {(4xy)^2}]\\ \Rightarrow (1 - 4xy)(1 + 4xy + 16{x^2}{y^2})\end{array}\]
3. Use the formula and evaluate (97)3
\[\begin{array}{l}{(97)^3} = {(100 - 3)^3}\\\end{array}\]
we know that \[{(a - b)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\]
a=100 and b=3
\[\begin{array}{l} \Rightarrow {(100)^3} - 3{(100)^2}(3) + 3(100){(3)^2} - {(3)^3}\\ \Rightarrow 1000000 - 90000 + 2700 - 27\\ \Rightarrow 912,673\end{array}\]
Therefore,\[{(97)^3} =912,673\]
Summary
The most widely used perfect cubes are those whose roots are integers rather than decimals. To factor the differences between the two perfect cubes, keep in mind that the variance of the cube roots of the two perfect cubes is equal to the product of their cube roots and the sum of their squares Binomial is the name for an algebraic expression with only two terms. It is a polynomial with two terms. It is also referred to as the sum or difference of two or more monomials.
FAQs on Cube of the Difference of Two Binomials Explained
1. What is the formula for the cube of the difference of two binomials?
The formula for the cube of the difference of two binomials is (a − b)³ = a³ − 3a²b + 3ab² − b³. This identity is derived using binomial expansion and follows a specific sign pattern.
- First term: cube of the first term → a³
- Second term: −3a²b
- Third term: +3ab²
- Last term: −b³
2. How do you expand (a − b)³ step by step?
To expand (a − b)³, use the binomial identity or multiply step by step to get a³ − 3a²b + 3ab² − b³.
- Step 1: Write (a − b)³ = (a − b)(a − b)(a − b)
- Step 2: First expand (a − b)(a − b) = a² − 2ab + b²
- Step 3: Multiply (a² − 2ab + b²)(a − b)
- Step 4: Combine like terms to get a³ − 3a²b + 3ab² − b³
3. What is an example of the cube of the difference of two binomials?
An example of the cube of the difference is (2x − 3)³ = 8x³ − 36x² + 54x − 27.
- Use the formula: (a − b)³ = a³ − 3a²b + 3ab² − b³
- Here, a = 2x and b = 3
- (2x)³ = 8x³
- −3(2x)²(3) = −36x²
- +3(2x)(3)² = +54x
- −3³ = −27
4. Why do the signs alternate in (a − b)³?
The signs alternate in (a − b)³ because the negative term −b affects every product during expansion. When applying the binomial theorem, powers of −b change signs depending on whether the exponent is odd or even.
- Odd powers of −b stay negative
- Even powers of −b become positive
5. What is the difference between (a − b)³ and (a + b)³?
The main difference between (a − b)³ and (a + b)³ is the sign pattern of the middle terms.
- (a + b)³ = a³ + 3a²b + 3ab² + b³
- (a − b)³ = a³ − 3a²b + 3ab² − b³
6. Can the cube of the difference formula be derived using the binomial theorem?
Yes, the cube of the difference formula comes directly from the binomial theorem. Using the theorem:
- (a − b)³ = C(3,0)a³ − C(3,1)a²b + C(3,2)ab² − C(3,3)b³
- Coefficients: 1, 3, 3, 1
7. What are common mistakes when expanding (a − b)³?
A common mistake when expanding (a − b)³ is writing incorrect signs or forgetting coefficients. Students often write a³ − b³, which is incorrect.
- Forgetting the middle terms (−3a²b and +3ab²)
- Using wrong signs for the third term
- Not cubing both a and b properly
8. How is the cube of the difference used in algebra problems?
The cube of the difference is used to simplify algebraic expressions and solve polynomial equations. It helps in expanding expressions like (x − 2)³ or factoring cubic polynomials.
- Simplifying algebraic identities
- Solving higher-degree equations
- Working with binomial expansions
9. How do you verify the expansion of (a − b)³?
You can verify the expansion of (a − b)³ by multiplying (a − b)(a − b)(a − b) directly to check if it equals a³ − 3a²b + 3ab² − b³.
- First multiply two binomials
- Then multiply the result by the third binomial
- Combine like terms carefully
10. Is there a shortcut to remember the cube of the difference formula?
Yes, a simple way to remember the cube of the difference formula is: “Cube the first, minus three times first squared second, plus three times first second squared, minus cube the last.” This gives (a − b)³ = a³ − 3a²b + 3ab² − b³.
- Coefficients follow 1, 3, 3, 1
- Signs alternate: −, +, −
