




How to Find the Base and Sides of an Isosceles Triangle
What is an Isosceles Triangle?
Triangles classified as isosceles have at least two sides with equal sides or angles. As three-sided unconstrained polygons, triangles are known to exist. Based on the length of their sides, triangles are called equilateral or isosceles.
No matter which way the triangle's peak (or apex) points, an isosceles triangle always has two equal sides. The following are some tips on isosceles triangles:
There are equal sides to it. The basis angles are two equal angles that make up the object.
A right isosceles triangle is one where the third angle is 90 degrees.
As we can see, the given figure \[OD = OC\] and \[\angle D\] are equal to \[\angle C\], so we can say that this given triangle is an isosceles triangle.
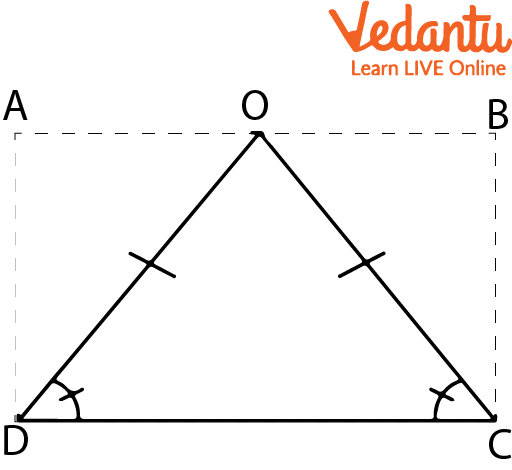
Isosceles Triangle
Properties of an Isosceles Triangle
The properties of the isosceles triangle are given below:
Two equal sides and two equal angles.
The two equal sides of an isosceles triangle are called the legs and the angle between them is called the vertex or apex angle.
The side opposite the vertex angle is called the base and base angles are equal.
The perpendicular from the apex angle bisects the base and the apex angle.
The perpendicular drawn from the apex angle divides the isosceles triangle into two congruent triangles and is also known as its line of symmetry.
Isosceles Triangle Diagram
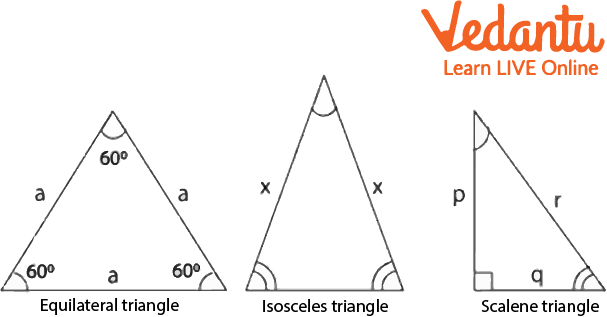
Three Types of Triangles
In the above figure, we can find the visual difference between the three different types of triangles to compare with an isosceles triangle. The first figure is of an equilateral triangle and second is an isosceles triangle and the last one is Scalene.
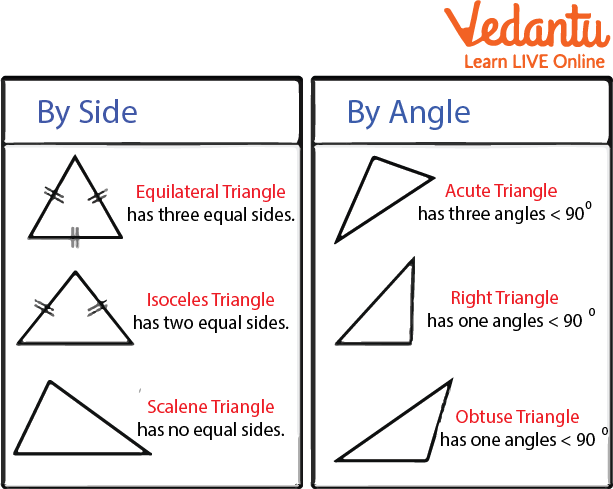
Different Triangles
In the above-given figure, we can see many types of triangles. All triangles given above state their features on their own. First three have their properties by sides, and the remaining three by their angles. Each triangle has its features and properties. As we can see in the diagram that equilateral triangle has three equal angles, the isosceles have two equal angles, and the scalene has no equal angles. Similarly, the acute triangle has three angles less than 90, and the right has only one angle equal to 90, and the obtuse has an angle of more than 90.
The Base of an Isosceles Triangle
A triangle with two equal-length sides is termed an isosceles triangle. The base refers to the triangle's third side. The angle between the legs is known as the vertex angle. The base angles are those angles that have the base as one of their sides.
Q. Given an isosceles triangle measure of the unequal angle is 70° and the other two equal angles measure x; then what is the value of x?
Ans: The given angle is 70.
\[{\bf{70}}^\circ {\rm{ }} + {\rm{ }}{\bf{x}}{\rm{ }} + {\rm{ }}{\bf{x}}{\rm{ }} = {\rm{ }}{\bf{180}}^\circ \]
\[{\bf{70}}^\circ {\rm{ }} + {\rm{ }}{\bf{2x}}{\rm{ }} = {\rm{ }}{\bf{180}}^\circ \]
\[{\bf{2x}}{\rm{ }} = {\rm{ }}{\bf{180}}{\rm{ }}-{\rm{ }}{\bf{70}}{\rm{ }} = {\rm{ }}{\bf{110}}^\circ \]
\[{\bf{x}}{\rm{ }} = {\rm{ }}\frac{{110}}{2}{\rm{ }} = {\rm{ }}{\bf{55}}^\circ \]
Hence, The value of x is 55.
Area of an Isosceles Triangle
The region that an isosceles triangle occupies in two dimensions is referred to as its area. Typically, the base and height of an isosceles triangle are divided by two to create the triangle. The following equation can be used to determine an isosceles triangle's area:
An isosceles triangle's area is A = ½* b* h square units.
Examples
Example 1: Calculate the area of an isosceles triangle given \[b{\rm{ }} = {\rm{ }}12{\rm{ }}cm\] and \[h{\rm{ }} = {\rm{ }}17{\rm{ }}cm\]?
Ans:
Given , \[b{\rm{ }} = {\rm{ }}12{\rm{ }}cm\]
\[h{\rm{ }} = {\rm{ }}17{\rm{ }}cm\]
Area of Isosceles Triangle \[ = {\rm{ }}\left( {1/2} \right){\rm{ }} \times {\rm{ }}b{\rm{ }} \times {\rm{ }}h\]
\[ = {\rm{ }}\left( {1/2} \right){\rm{ }} \times {\rm{ }}12{\rm{ }} \times {\rm{ }}17\]
\[ = {\rm{ }}6{\rm{ }} \times {\rm{ }}17\]
\[ = {\rm{ }}102{\rm{ }}c{m^2}\]
Example 2: Find the length of the base of an isosceles triangle whose area is\[243{\rm{ }}c{m^2}\], and the altitude of the triangle is \[27{\rm{ }}cm.\]
Ans: Area of the triangle is \[243{\rm{ }}c{m^2}\]
Height of the triangle is \[27{\rm{ }}cm\]
The base of the triangle = b =?
Area of Isosceles Triangle is \[\left( {1/2} \right){\rm{ }} \times {\rm{ }}b{\rm{ }} \times {\rm{ }}h\]
\[243{\rm{ }} = {\rm{ }}\left( {1/2} \right){\rm{ }} \times {\rm{ }}b{\rm{ }} \times {\rm{ }}27\]
\[243{\rm{ }} = {\rm{ }}\left( {b \times 27} \right)/2\]
\[b{\rm{ }} = {\rm{ }}\left( {243 \times 2} \right)/27\]
\[b{\rm{ }} = {\rm{ }}18{\rm{ }}cm\]
Hence, the base of the triangle is 18 cm.
Summary
In this article, we have covered various topics regarding isosceles triangles. We understood that the basic properties of the triangle are that both the sides and angles are equal. We have also solved the examples and solved questions to understand them better.
FAQs on Base of an Isosceles Triangle Explained
1. What is the definition of an isosceles triangle?
An isosceles triangle is a type of triangle that has at least two sides of equal length. These equal sides are often called 'legs'. Consequently, the two angles opposite these equal sides are also equal in measure.
2. What is the base of an isosceles triangle?
In an isosceles triangle, the base is the third side, which is typically the one with a different length from the other two equal sides. The angles at either end of the base are called the base angles, and they are always equal to each other.
3. What is the difference between an isosceles triangle and an isosceles right-angled triangle?
The primary difference lies in their angles.
- An isosceles triangle must have two equal sides and two equal base angles. The third angle can be acute, right, or obtuse.
- An isosceles right-angled triangle is a specific type of isosceles triangle where one of the angles is exactly 90 degrees (a right angle). This means the other two angles must be 45 degrees each.
4. How do you find the area of an isosceles triangle if you know the base length?
To find the area of an isosceles triangle, you can use the formula: Area = (1/2) × base × height. If the height is not known, you must first calculate it by drawing an altitude from the vertex angle to the base. This altitude bisects the base, creating two right-angled triangles. You can then find the height using the Pythagorean theorem.
5. What does the Base Angle Theorem state for an isosceles triangle?
The Base Angle Theorem is a fundamental property of isosceles triangles. It states that if two sides of a triangle are congruent (equal in length), then the angles opposite those sides are also congruent (equal in measure). These equal angles are the base angles.
6. Can any of the three sides of an isosceles triangle be considered the base?
While mathematically you can choose any side as a 'base' for an area calculation (provided you know the corresponding perpendicular height), the term 'base' in the context of an isosceles triangle's unique properties specifically refers to the side that is not equal to the other two. This convention makes discussing properties like the Base Angle Theorem and symmetry clear and consistent.
7. Why are the base angles of an isosceles triangle always equal?
The equality of base angles can be explained by symmetry. If you draw a line segment (an altitude) from the vertex angle (the angle between the two equal sides) perpendicular to the base, it divides the isosceles triangle into two smaller, identical right-angled triangles. Because these two triangles are congruent (by the Hypotenuse-Leg or Side-Angle-Side rule), all their corresponding parts, including the angles, must be equal. This proves that the two base angles are equal.
8. What are some real-world examples that use the structure of an isosceles triangle and its base?
The isosceles triangle structure is common in engineering and design for its stability. Examples include:
- Architectural Trusses: The gabled end of a house roof often forms an isosceles triangle, where the horizontal beam is the base.
- Bridges: Many truss bridge designs use repeating isosceles triangles for strength and load distribution.
- Household Items: A simple coat hanger is a great example, with the horizontal bar acting as the base.
- Traffic Signs: The standard 'yield' sign is an equilateral triangle, which is a special type of isosceles triangle where all three sides (and angles) are equal.

















