Adjacent Angles and Common Vertex

There are numerous examples of adjacent angles in regular activities. The most typical real-world example of adjacent angles is two pizza slices next to one another. The hour, minute, and second hands on a clock, which, when all three are separated from one another, form adjacent angles. The steering wheel of a car has three adjacent angles that we can locate. When two angles are next to each other, the angle created by two non-common arms and one common arm constitutes their sum. Angles that are always placed next to one another, sharing a common vertex and common side but not overlapping, are said to be adjacent angles.

Common Vertex

A vertex that is shared by two angles is known as a common vertex. In other words, the intersection of any two linear structures (like line, line segment, ray) is known as a vertex. Vertices are found at the points where parallel lines and transversals cross, in the corners of polygons, and as the central angles of circles.

Common Side

Two angles having the same vertex can have a common side, which can be a line, ray, or line segment. The common side and one other side are used by both angles.

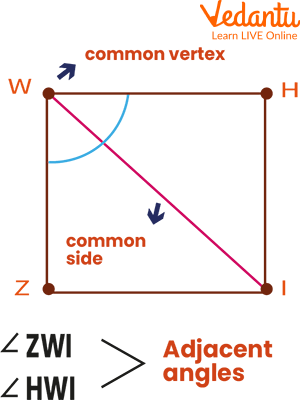
Common vertex and Common side

What are Adjacent Angles?

Angles that are always placed next to one another, sharing a common vertex and common side but not overlapping, are said to be adjacent angles. So, we can say that a common vertex point is required for making an adjacent angle. In its simplest form, we can say that angles that have a common vertex and side but not overlapping are termed adjacent angles.

Adjacent angles can be distinguished by these characteristics:

1. The common vertex exists.

2. The common side exists.

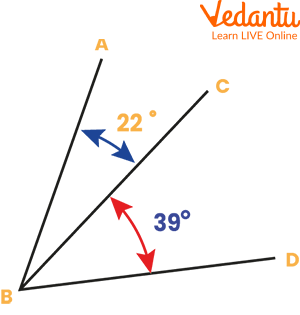
Adjacent Angles

In the above image angles, ABC and CBD are adjacent angles because:

There is a common side that is line CB.

There is a common vertex B.

Examples of Adjacent Angles

Linear Pair

You must try to imagine a cross to fully understand the look of a linear pair. So, four angles are formed when two lines cross. Below image showing two opposite rays with a common vertex.

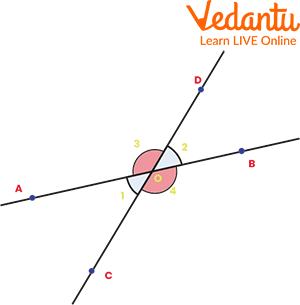
Linear Pair

The image above shows four angles with the numbers 1, 2, 3, and 4 written next to them. The linear angles in this cross are 1 and 3, 3 and 2, 2 and 4, 4 and 1.

If two angles add up to 180 degrees is a second way to confirm that they are a linear pair. Each pair of supplementary linear angles always sums to 180 degrees.

Vertically Opposite Angles

Even though they are technically not adjacent angles, vertically opposite angles are usually present where adjacent angles are.

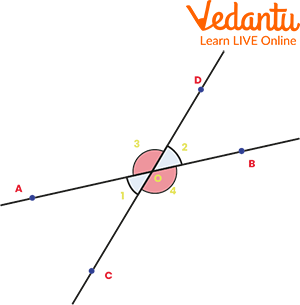
Vertical opposite angles

Although they have already been discussed, vertical angles only have one vertex in common and no common sides. If we look at the image above, the angles 3 and 4 and 1 and 2 are viewed as being vertically opposite. The fact that they measure the same is a significant necessity for vertically opposite angles. As an illustration, if angle 1 measures 60 degrees, angle 2 would also be 60 degrees.

Solved Examples

Example 1: Identify all the adjacent angles in the given figure.

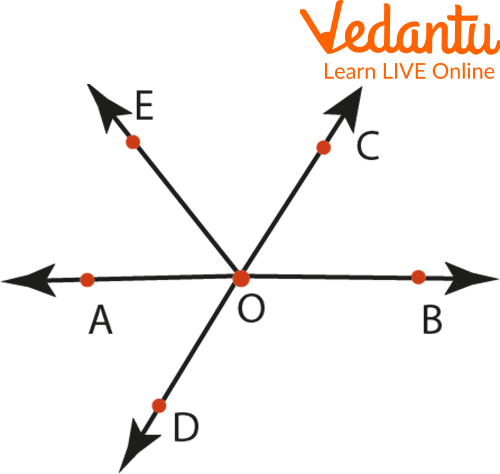
Adjacent angles

Ans: Here adjacent angles are:

$\angle \mathrm{AOE}$ and $\angle \mathrm{EOC}$

$\angle \mathrm{E O C}$ and $\angle \mathrm{C O B}$

$\angle \mathrm{C O B}$ and $\angle \mathrm{B O D}$

$\angle \mathrm{B O D}$ and $\angle \mathrm{A O D}$

$\angle \mathrm{A O D}$ and $\angle \mathrm{A O E}$

Example 2: Find the values of $x$ and $y$ since $AOC$ and $BOC$ form a linear pair if $x-y=$ $60^{\circ}$.

Ans: We have given that $x-y=60^{\circ} \ldots$ (i)

We are aware that $x+y=180^{\circ} \ldots$..(ii)

By multiplying (i) and (ii), we get

$2 \mathrm{x}=240^{\circ}$

$\left(240^{\circ} / 2\right)$

$x=120^{\circ} \text {. }$

Therefore,

$120^{\circ}-y=60^{\circ}$

$-y=60^{\circ}-120^{\circ}$

$-y=-60^{\circ}$

$y=60^{\circ}$

Example 3: Identify all the adjacent angles in the given figure.

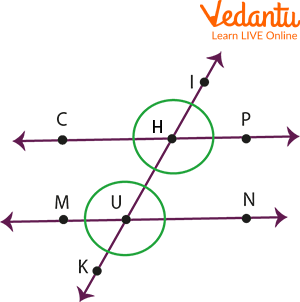
Adjacent angles

Ans: Here we have the following adjacent angles:

$\angle \mathrm{CHI}$ and $\angle \mathrm{PHI}$

$\angle \mathrm{CHI}$ and $\angle \mathrm{CHU}$

$\angle \mathrm{PHI}$ and $\angle \mathrm{PHU}$

$\angle \mathrm{C H U}$ and $\angle \mathrm{P H U}$

$\angle \mathrm{M U K}$ and $\angle \mathrm{NUK}$

$\angle \mathrm{MUH}$ and $\angle \mathrm{NUH}$

$\angle \mathrm{MUH}$ and $\angle \mathrm{MUK}$

$\angle \mathrm{NUH}$ and $\angle \mathrm{NUK}$

Practice Problem

Q. Are the angles shown below adjacent? Give justifications.

Practice Question

Answer:

1.

(a) No.

(b) No.

(c) No.

(d) Yes.

Summary

In this article we learned that Angles that are always placed next to one another, sharing a common vertex and common side but not overlapping, are said to be adjacent angles. The sum of the adjacent angles formed when a ray is in a straight line is 180°. A linear pair of angles is defined as two adjacent angles whose sum is 180 degrees. Due to the fact that supplementary angles add up to 180°, all linear pairs are supplementary. The supplementary angles do not all have to be linear pairs, though. The lines must cross each other and form adjacent angles in order to form a linear pair. The non-common arms form a line if the product of any two adjacent angles is a straight line.