Simplest Form

The Concept of Simplest Form in Math

You might have heard of fractions and in that concept, there is a term called equivalent fractions, so what are fractions? Firstly, we need to understand this.

Let us assume that your father brought three packets of Dairy milk chocolate. One packet of chocolate has 12 slices, so your father distributes half of the slices to you and the other half to your sibling. In this way, you and your brother have 6 parts out of 12. Now, if we wish to represent your share in a fraction, we have 6/12 each for you and your brother. Furthermore, we simplify $\frac{6}{12}=\frac{1}{2}$, and notice that half part of the chocolate is given to you and the other half to your brother.

So, when we simplify any big number into the shortest form possible, we call the obtained fraction the simplest form, like the simplest form of $\frac{6}{12}=\frac{1}{2}$.

Also, we will look at various examples to understand what is the simplest form. 

Simplest Form in Fractions

Do you know what the simplest form is? Well, it is just like simplifying a fraction, as we understood in the above example. Now, let us find the simplest form of fractions.

• $\frac{144}{336}$

Now, $\frac{144}{336}=\frac{36}{84}=\frac{9}{21}=\frac{3}{7}$

So, here the simplest form of $\frac{144}{336}$ is $\frac{3}{7}$. 

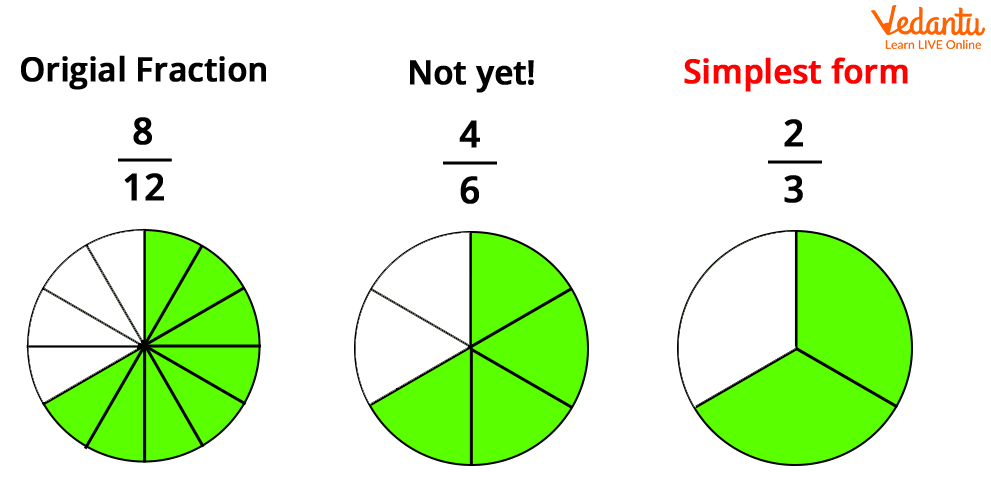
• $\frac{150}{225}$

Now, $\frac{150}{225}=\frac{10}{15}=\frac{2}{3}$

So, the simplest form of $\frac{150}{225}$ is $\frac{2}{3}$.

• $\frac{198}{234}$

Here, $\frac{198}{234}=\frac{66}{78}=\frac{23}{26}=\frac{11}{13}$

So, the simplest form of $\frac{198}{234}$ is $\frac{11}{13}$.

• $\frac{200}{550}$

Here, $\frac{200}{550}=\frac{20}{55}=\frac{4}{11}$

So, the simplest form of a fraction is $\frac{4}{11}$.

Here, if you notice one thing in the above examples, $\frac{144}{336}$can be written as $\frac{36}{84}$ or $\frac{9}{21}$  or $\frac{3}{7}$ . Thus, $\frac{36}{84}$ , $\frac{9}{21}$ , and $\frac{3}{7}$  are equivalent fractions of $\frac{144}{36}$ .

Also, we can notice that  $\frac{36}{84}$ , $\frac{9}{21}$ , and $\frac{3}{7}$  are proper fractions, but how? Let us understand this part.

Here, in $\frac{36}{84}$ , 36 is a numerator, 84 is a denominator, and 36 < 84. This means that the numerator is lesser than the denominator and when this is the case, we call this fraction a proper fraction.  Now, let us take an example of a fraction having a numerator greater than the denominator.

Example 1: $\frac{350}{175}$ 

Here, $\frac{350}{175}=\frac{50}{25}=\frac{2}{1}$

Here, equivalent fractions of $\frac{350}{175}$ are $\frac{50}{25}$ and $\frac{2}{1}$. Also, these fractions have a numerator greater than the numerator, like you can see that 350 > 175, 50 > 25, and 2 > 1. Besides this, the simplest form of the above fraction is $\frac{2}{1}$.

From the above text, we conclude that the simplest form of the proper and improper fraction is similar to the concept of equivalent fractions. Also, we can substitute either of the fractions if we get any questions to solve.