Addition Concept

The addition is a mathematical operation. They are methods and tasks related to numbers. It can be described by combining two or more numbers or adding two or more numbers. It is one of four arithmetic operations along with subtraction, multiplication, and division.

How Can Addition be Performed?

Let's start with an example. 7 + 4 means combining the numbers 7 and 4 to get the solution. The result, as you know, is 11. Sums can be divided into terms and sums. A term is a number added, and the answer to addition is a sum. To solve the sum, the terms must be joined together. So the expression 7 + 4 = 11 can be written as:

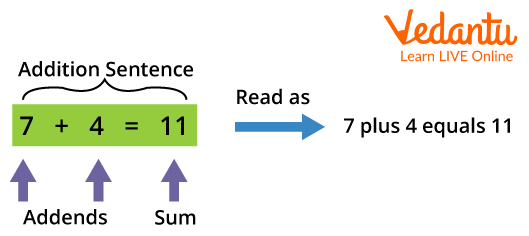
Example of Addition

Different Methods of Addition

Now we will learn about different ways by which we can solve addition problems:

• Go to Visualizations: Comprehension can be improved by using pictorial totals or having students draw countable objects
  
  

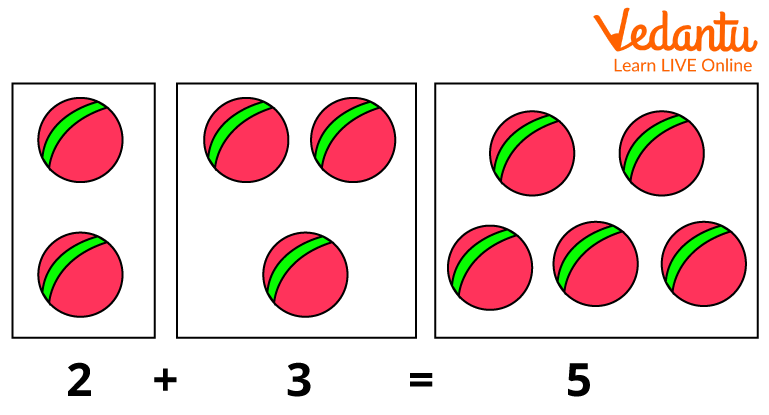
Addition with Countable Objects

• Addition Using a Number Line: A number line is a horizontal line that has numbers placed at equal intervals.

• Number Lines help simplify the calculation process.

• For example, if the sum is 3 + 4, the child can first count to three digits then by placing four fingers to get 7. You don't have to count to 3 first to find the solution.

Addition Using Number Line

• Counting: As your child gets used to the number strings, you will want to use the same strategy in their head. Counting your fingers out loud will help you gain.

More about Addition Concept

The addition operator can be divided into the following parts:

• Addend: The numbers being added are called addition.

• Plus Sign: There is a plus sign \[[ + ]\] between additions.

• If the statement is written horizontally, place an equal sign \[[ = ]\] just before the sum item.

• Sum: The final result after adding terms is called the sum.

Addition Examples Worksheet

Add the following examples:

1. \[\textbf{2 + 2 = }\]

Ans: Here we have to add the terms which are 2 and 2 so on combining 2 and 2 together we get a sum of 4.

Therefore, \[2 + 2 = 4\]

2. \[\textbf{9 + 0 = }\]

Ans: Here we need to combine 9 and 0 so on combining 9 and 0 we get the sum as 9.

Therefore, \[9 + 0 = 9\]

3. \[\textbf{8 + 2 =} \]

Ans: As above problems , \[8 + 2 = 10\]

4. \[\textbf{4 + 4 = }\]

Ans: Sum of \[4 + 4 = 8\].

5. \[\textbf{2 + 9 = }\]

Ans: Therefore, Sum will be 11.

Conclusion

Addition is the mathematical operation that defines the sum or total of quantities. The addition operator is plus (+) sign. We have learnt about the concept of addition in this article and we have studied various methods by which addition can be done. You can now apply your understanding of addition in solving the worksheet given below.