
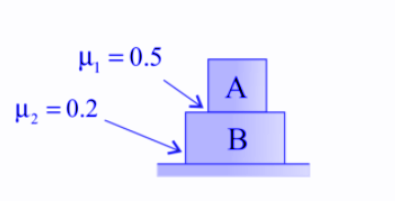
What is the value of acceleration of blocks A and B if F = 40N and mass of block A is 5 kg and mass of block B is 10 kg? The arrangement of two blocks is shown below in the figure.
Answer
215.7k+ views
Hint At first, find the value of limiting friction on all contact surfaces which is denoted by ${f_{s\max }}$.
Then, by using the below formula, find out the acceleration for both blocks one by one from given values in question,
$\Rightarrow F - {f_{s\max }} = ma$
where, ${f_{s\max }} = $limiting value of friction
$m = $mass of a block
$a = $acceleration of a block.
Complete step by step Solution
The force which opposes motion of an object moving relative to another is called Friction. It is not a fundamental force.
The maximum value of static friction that occurs when the body is just at the sliding point of the surface of another body. In other words, we can say that it is a product of coefficients of limiting friction and normal force. We can express it mathematically as,
$\Rightarrow {f_{s\max }} = \mu N$
Normal force can also be written as,
$\Rightarrow$ $N = mg$(where, $g = 10m{s^{ - 2}}$)
To find out the acceleration from limiting friction we need to use the below expression,
$\Rightarrow$ $F - {f_{s\max }} = ma \cdots (1)$
So, let ${m_a}$ and ${m_b}$ be the mass of blocks A and B respectively and let ${a_a}$ and ${a_b}$ be the acceleration of blocks A and B respectively.
So, at first, we will find the acceleration for block A
Therefore, from equation $(1)$ we get,
$\Rightarrow F - {f_{s\max }} = {m_a}{a_a} $
$\Rightarrow F - \mu \times N = {m_a}{a_a} $
$\Rightarrow F - \mu \times {m_a}g = {m_a}{a_a} $
$\Rightarrow 40 - 0.5 \times 5 \times 10 = 5{a_a} $
$\Rightarrow 40 - 25 = 5{a_a} $
$\Rightarrow 15 = 5{a_a} $
$\Rightarrow {a_a} = 3m/{s^2} $
Let ${N'}$ be the force acting upon block A from block B -
$\therefore {N'} = N + {m_b}g$
So,
$\Rightarrow {\mu _1}N - {\mu _2}N' = {m_b}{a_b} $
$\Rightarrow 0.5 \times 50 - 0.2(50 + 10 \times 10) = 10{a_b} $
$\Rightarrow 25 - 0.2(150) = 10{a_b} $
$\Rightarrow 25 - 30 = 10{a_b} $
$\Rightarrow {a_b} = \dfrac{{ - 5}}{{10}}m/{s^2} $
So, the acceleration of block B is nearly 0.
Note Limiting friction occurs when the body is just at sliding point over another’s body surface. Limiting friction always opposes the motion of an object. When the surfaces are in contact, the limiting friction always acts tangentially to them.
Then, by using the below formula, find out the acceleration for both blocks one by one from given values in question,
$\Rightarrow F - {f_{s\max }} = ma$
where, ${f_{s\max }} = $limiting value of friction
$m = $mass of a block
$a = $acceleration of a block.
Complete step by step Solution
The force which opposes motion of an object moving relative to another is called Friction. It is not a fundamental force.
The maximum value of static friction that occurs when the body is just at the sliding point of the surface of another body. In other words, we can say that it is a product of coefficients of limiting friction and normal force. We can express it mathematically as,
$\Rightarrow {f_{s\max }} = \mu N$
Normal force can also be written as,
$\Rightarrow$ $N = mg$(where, $g = 10m{s^{ - 2}}$)
To find out the acceleration from limiting friction we need to use the below expression,
$\Rightarrow$ $F - {f_{s\max }} = ma \cdots (1)$
So, let ${m_a}$ and ${m_b}$ be the mass of blocks A and B respectively and let ${a_a}$ and ${a_b}$ be the acceleration of blocks A and B respectively.
So, at first, we will find the acceleration for block A
Therefore, from equation $(1)$ we get,
$\Rightarrow F - {f_{s\max }} = {m_a}{a_a} $
$\Rightarrow F - \mu \times N = {m_a}{a_a} $
$\Rightarrow F - \mu \times {m_a}g = {m_a}{a_a} $
$\Rightarrow 40 - 0.5 \times 5 \times 10 = 5{a_a} $
$\Rightarrow 40 - 25 = 5{a_a} $
$\Rightarrow 15 = 5{a_a} $
$\Rightarrow {a_a} = 3m/{s^2} $
Let ${N'}$ be the force acting upon block A from block B -
$\therefore {N'} = N + {m_b}g$
So,
$\Rightarrow {\mu _1}N - {\mu _2}N' = {m_b}{a_b} $
$\Rightarrow 0.5 \times 50 - 0.2(50 + 10 \times 10) = 10{a_b} $
$\Rightarrow 25 - 0.2(150) = 10{a_b} $
$\Rightarrow 25 - 30 = 10{a_b} $
$\Rightarrow {a_b} = \dfrac{{ - 5}}{{10}}m/{s^2} $
So, the acceleration of block B is nearly 0.
Note Limiting friction occurs when the body is just at sliding point over another’s body surface. Limiting friction always opposes the motion of an object. When the surfaces are in contact, the limiting friction always acts tangentially to them.
Recently Updated Pages
Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Correction Window 2026 Session 1 Dates Announced - Edit Form Details, Dates and Link

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

How to Convert a Galvanometer into an Ammeter or Voltmeter




