Question

Two straight roads OA and OB intersect at O. A tower is situated within the angles formed by them and subtends angles of \[{45^0}\]and \[{30^0}\]at the points A and B where the roads are nearest to it. If OA=a and OB=b, then the height of the tower is
A.\[\dfrac{{\sqrt {({a^2} + {b^2})} }}{2}\]
B.\[\sqrt {({a^2} + {b^2})} \]
C. \[\dfrac{{\sqrt {({a^2} - {b^2})} }}{2}\]
D. \[\sqrt {({a^2} - {b^2})} \]

Answer 1

Hint: By using Pythagorean theorem which gives the relation between hypotenuse, perpendicular and base of a right angled triangle we can find the height of the tower. Also here apply trigonometric identities.

Formula used: In right angled triangle, by Pythagorean theorem
\[{H^2} = {P^2} + {B^2}\]
Where H is hypotenuse
P is perpendicular
B is base

Complete step-by-step solution: Given OA = a, OB = b

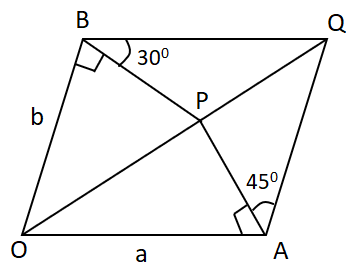
Image: A tower is situated within the angles of \[{45^0}\]and \[{30^0}\]at the points A and B
Let PQ be the tower of height h and PA, PB be the perpendicular from top of the tower P upon OA & OB respectively.
In figure \[\angle PBQ = {30^o}{\rm{ and }}\angle {\rm{PAQ = 4}}{{\rm{5}}^0}\]
 In
\[\begin{array}{l}\cot {45^0} = \dfrac{{base}}{{perpendicular}}\\{\rm{ 1 = }}\dfrac{{PA}}{h}{\rm{ (cot4}}{{\rm{5}}^0} = 1)\end{array}\]
PA = h
In
\[\begin{array}{l}\cot {30^0} = \dfrac{{base}}{{perpendicular}}\\{\rm{ }}\sqrt 3 {\rm{ = }}\dfrac{{PB}}{h}{\rm{ (cot3}}{{\rm{0}}^0} = \sqrt 3 )\end{array}\]
PB =\[\sqrt 3 {\rm{ h}}\]
Now In\[\Delta OPA\], by Pythagorean theorem
\[{H^2} = {P^2} + {B^2}\]
\[O{P^2} = P{A^2} + O{A^2} = P{B^2} + O{B^2}\]
Substituting all the values, we get
$h^2 + a^2 = 3h^2 + b^2$
$2h^2 = a^2 – b^2$
h = \[\dfrac{{\sqrt {({a^2} - {b^2})} }}{2}\]
Therefore the height of the tower is\[\dfrac{{\sqrt {({a^2} - {b^2})} }}{2}\]
Hence option C is the correct answer.

Note:If two right angled triangles form with the same perpendicular side, then we can use Pythagoras theorem for both triangles and equate them to get the same perpendicular side. In mathematics, the Pythagorean theorem or also known as Pythagoras theorem is a fundamental relation in geometry among the three sides of a right-angled triangle.