Question

Two resistors 3ohm and 2ohm are connected in parallel and a potential difference of 12V is connected across them. Find:
(A) The equivalent resistance of the parallel combination of the resistors.
(B) The current through the circuit.
(C) The current through each branch.

Answer 1

Hint: For the above problem we will keep a few points in mind:
1. Parallel connection has the same voltage throughout the circuit. Current will be different in each branch of the circuit if the connection is in parallel.
2. Equivalent resistance of the circuit can be found by determining the ratio of multiplication of the circuit to the total sum of the resistances.

Complete step by step solution:
Let’s complete the first part of the problem:

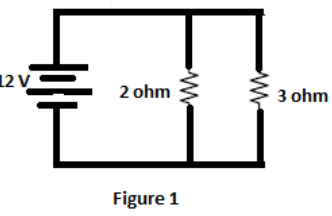
(A) In the above figure 2 ohm and 3 ohm resistors are connected in parallel and in parallel connection equivalent resistance have the value of ratio of product of the two resistors to the sum of two resistors.
$\Rightarrow {R_{eq}} = \dfrac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}} $
$ \Rightarrow {R_{eq}} = \dfrac{{2 \times 3}}{{2 + 3}} $
(We wrote the formula and substituted the values of each resistor)
$ \Rightarrow {R_{eq}} = \dfrac{6}{5}$ ohm
Value of the parallel combination is 1.2 ohm.
Now, we will solve the part b of the problem

(B) Total current in the circuit is given by Ohm’s law, which is stated as:
$V = IR$
Total Voltage = 12V
Total resistance =1.2 ohm
$ \Rightarrow I = \dfrac{V}{R} $
$ \Rightarrow I = \dfrac{{12}}{{1.2}} $
(Value of total current in the circuit)
$ \Rightarrow I = 10A$
Last part of the solution, now

(C) Current in each branch is given as:
Voltage of each branch will be 12 V, therefore current of 2 ohm is:
$ \Rightarrow {I_{2ohm}} = \dfrac{{12}}{2} = 6A$ (Current in 2 ohm resistor)
$ \Rightarrow {I_{3ohm}} = \dfrac{{12}}{3} = 4A$ (Current in 3 ohm resistor)
We can cross verify our results that the total current of the circuit is 10 A and the current in each branch is also 10A.

Note: When the resistors are connected in series, current throughout the circuit will remain the same but the voltage will be different. Current through each resistor will be the same and voltage will be different across each resistor and the total voltage will be equal to the sum of the voltages across each resistor.