Question

Two ions having masses in the ratio $1:1$ and charges $1:2$ are projected into uniform magnetic field perpendicular to the field with speeds in the ratio $2:3$.The ratio of the radii of circular paths along which the two particles move is
A.$4:3$
B.$2:3$
C.$3:1$
D.$1:4$

Answer 1

Hint: When a charged particle moves in a direction of uniform magnetic field and then velocity of the particle experiences a perpendicular magnetic force. In this case magnetic force becomes centripetal force due to its direction towards the circular path of radius $r$ of the charged particle.



Formula used:
Radius,$r$ of the circular path described by the particle in the following way:
$r=\dfrac{mv}{qB}$
Here $m=$mass of the particle
$v=$ speed of the moving particle
$q=$ charge of the particle
$B=$ magnetic field


Complete answer:
When a particle carrying charge $q$ moves in the presence of a uniform magnetic field ($\vec{B}$) the magnetic force becomes perpendicular to the velocity $\vec{v}$ of the particle.

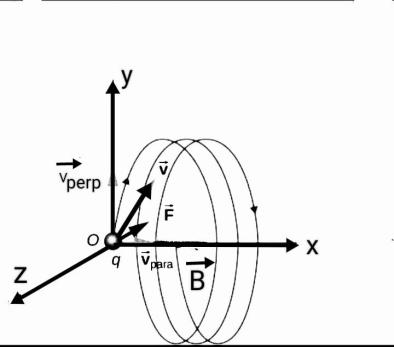
Hence mathematically this can cab expressed in the following way:
$F=q(\vec{v}\times \vec{B})$ …..(i)
Now this magnetic force acts like centripetal force due to its direction towards the circular motion of the particle. This can be expressed by the following way:
$F=\dfrac{m{{v}^{2}}}{r}$ …..(ii)
Here $m=$mass of the particle
$r=$radius of circular path
From (i), $F=q(vB\sin \theta )$
Or,$F=q(vB\sin {{90}^{o}})$ [since angle$\theta ={{90}^{o}}$ as $\vec{B}$ is perpendicular to $\vec{v}$]
Or,$F=qvB$ …...(iii)
By equating (ii) and (iii) we get,
$\dfrac{m{{v}^{2}}}{r}=qvB$
Or,$r=\dfrac{mv}{qB}$ …….(iv)
Now if there are two ions having masses ${{m}_{1}}\And{{m}_{2}}$ and charges ${{q}_{1}}\And{{q}_{2}}$ are projected into uniform magnetic field$B$ with speeds ${{v}_{1}}\And{{v}_{2}}$ , then we can write radius equation for two ions in the following ways,
${{r}_{1}}=\dfrac{{{m}_{1}}{{v}_{1}}}{{{q}_{1}}B}$ …….(v)
${{r}_{2}}=\dfrac{{{m}_{2}}{{v}_{2}}}{{{q}_{2}}B}$ ……..(vi)
Dividing (v) and (vi) we get,
$\dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{{{m}_{1}}{{v}_{1}}}{{{q}_{1}}B}\times \dfrac{{{q}_{2}}B}{{{m}_{2}}{{v}_{2}}}$
Or,$\dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{{{m}_{1}}}{{{m}_{2}}}\times \dfrac{{{v}_{1}}}{{{v}_{2}}}\times \dfrac{{{q}_{2}}}{{{q}_{1}}}$
Given,$\dfrac{{{m}_{1}}}{{{m}_{2}}}=\dfrac{1}{1}$,$\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{2}{3}$,$\dfrac{{{q}_{1}}}{{{q}_{2}}}=\dfrac{1}{2}$
Putting these value in the above equation we get ratio or radii of circular path,
$\therefore \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{1}{1}\times \dfrac{2}{3}\times \dfrac{2}{1}=\dfrac{4}{3}$
Hence the ratio of radii of circular path along which the two particles move is $4:3$.

Thus, option (A) is correct.




Note:In a situation when magnetic field and velocity are parallel to each other then the particle does not experience any magnetic force . As a result the magnitude of force remains constant in the entire motion that no magnetic field is felt upon it.