Question

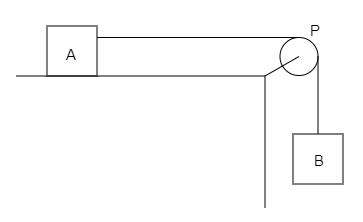
Two blocks $A$ and $B$ are arranged as shown in the figure. The mass of the block $A$ is $10\,kg$. The coefficient of friction between the block $A$ and the horizontal plane is $0.2$. The minimum mass of block $B$ to start motion will be:



(A) $0.2\,kg$
(B) $10\,kg$
(C) $5\,kg$
(D) $2\,kg$

Answer 1

Hint The mass of the block $B$ can be determined by the force of the block $B$ is equated with the friction force of the block $A$. The friction force of the block $A$ can be determined by the product of the force of the block $A$ and the coefficient of the friction of the surface of the block $A$.
Useful formula
The friction force of the block $A$ is given by,
$f = {F_A} \times \mu $
Where, $f$ is the frictional force of the block $A$, ${F_A}$ is the force of the block $A$ and $\mu $ is the coefficient of the friction of the block $A$.

Complete step by step solution
Given that,
The mass of the block $A$ is, ${m_A} = 10\,kg$,
The coefficient of the friction is, $\mu = 0.2$.
Now, the force of the block $A$ is given by,
${F_A} = {m_A} \times g$
Where, $g$ is the acceleration due to gravity.
By assuming the acceleration due to gravity is $g = 10\,m{s^{ - 2}}$ and substitute the mass value in the above equation, then
${F_A} = 10 \times 10$
By multiplying the terms in the above equation, then the above equation is written as,
${F_A} = 100\,N$
Now, the friction force of the block $A$ is given by,
${f_A} = {F_A} \times \mu $
By substituting the force of the block $A$ and the coefficient of the friction in the above equation, then the above equation is written as,
\[{f_A} = 100 \times 0.2\]
By multiplying the terms in the above equation, then the above equation is written as,
\[{f_A} = 20\,N\]
Now, the force of the block $B$ is given by,
${F_B} = {m_B} \times g$
By equating the force of the block $B$ and the friction force of the block $A$ , then
\[20 = {m_B} \times g\]
By rearranging the terms in the above equation, then the above equation is written as,
\[{m_B} = \dfrac{{20}}{g}\]
By assuming the acceleration due to gravity is $g = 10\,m{s^{ - 2}}$ and substitute in the above equation, then
\[{m_B} = \dfrac{{20}}{{10}}\]
By dividing the terms in the above equation, then the above equation is written as,
\[{m_B} = 2\,kg\]

Hence, the option (D) is the correct answer.

Note The fore of the object is directly proportional to the mass of the object and the acceleration due to gravity of the object. The frictional force of the object is directly proportional to the force of the object and the coefficient of the friction of the object.