
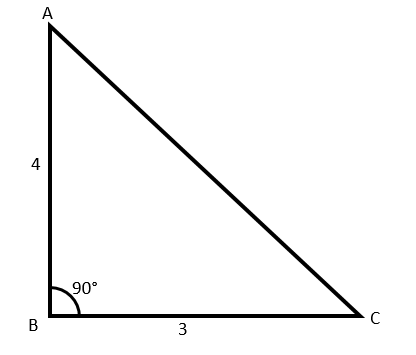
There is a flat uniform triangular plate ABC such that \[AB = 4cm\], \[BC = 3cm\]and \[\angle ABC = 90^\circ \]as shown in the figure. The moment of inertia of the plate about AB, BC and CA is I1, I2 and I3 respectively. The incorrect statement is,
A.\[{I_3} < {I_2}\]
B. \[{I_2} < {I_1}\]
C. \[{I_3} < {I_1}\]
D. \[{I_3} > {I_2}\]
Answer
217.8k+ views
Hint:The moment of inertia is the product of the mass and the square of the distance of the mass from the axis of rotation. As we increase the distance the moment of inertia increases. So, the mass distribution in which the mass is located near the axis of rotation is having the least moment of inertia.
Formula used:
Distance of point \[\left( {{x_1},{y_1}} \right)\]from the line \[ax + by + c = 0\] is given as,
\[d = \left| {\dfrac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|\]
\[\Rightarrow {x_{com}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{x_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}\]
\[\Rightarrow {y_{com}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}\]
Here, \[{x_{com}}\] and \[{y_{com}}\] is the x and y coordinate of the centre of mass.
Complete step by step solution:
The coordinate of the centre of mass of the given right triangular plate can be determined as,
\[{x_{com}} = \dfrac{{0 + 0 + 3}}{3} = 1\]
\[\Rightarrow {y_{com}} = \dfrac{{0 + 4 + 0}}{3} = \dfrac{4}{3}\]
So, the coordinate of the centre of mass of the given plate is \[\left( {1,\dfrac{4}{3}} \right)\].
The distance of the centre of mass from the side AB is \[{d_{AB}} = 1\]
The distance of the centre of mass from the side BC is \[{d_{BC}} = \dfrac{4}{3}\]
The equation of the line AC is,
\[y - 4 = \dfrac{{0 - 4}}{{3 - 0}}\left( {x - 0} \right) \Rightarrow y = - \dfrac{4}{3}x + 4\]
So, the side AC is along \[4x + 3y - 12 = 0\]
The distance of the centre of mass from the side CA is,
\[{d_{CA}} = \left| {\dfrac{{\left( {4 \times 1} \right) + \left( {3 \times \dfrac{4}{3}} \right) - 12}}{{\sqrt {{4^2} + {3^2}} }}} \right|\]
\[\Rightarrow {d_{CA}} = \dfrac{4}{5}\]

Image: The right triangular plate in cartesian coordinate system.
The order of the distance of the centre of mass of the right triangular plate from the sides is as,
\[{d_{Bc}} > {d_{AB}} > {d_{CA}}\]
As the moment of inertia is proportional to the square of the distance of the centre of mass from the axis of rotation,
\[{I_2} > {I_1} > {I_3}\]
Hence, the statement \[{I_3} > {I_2}\] is incorrect.
Therefore,the correct option is (D).
Note: The moment of inertia about the smaller side of the triangular lamina is maximum because the effective distance of the centre of mass is from the axis of rotation is maximum.
Formula used:
Distance of point \[\left( {{x_1},{y_1}} \right)\]from the line \[ax + by + c = 0\] is given as,
\[d = \left| {\dfrac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|\]
\[\Rightarrow {x_{com}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{x_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}\]
\[\Rightarrow {y_{com}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}\]
Here, \[{x_{com}}\] and \[{y_{com}}\] is the x and y coordinate of the centre of mass.
Complete step by step solution:
The coordinate of the centre of mass of the given right triangular plate can be determined as,
\[{x_{com}} = \dfrac{{0 + 0 + 3}}{3} = 1\]
\[\Rightarrow {y_{com}} = \dfrac{{0 + 4 + 0}}{3} = \dfrac{4}{3}\]
So, the coordinate of the centre of mass of the given plate is \[\left( {1,\dfrac{4}{3}} \right)\].
The distance of the centre of mass from the side AB is \[{d_{AB}} = 1\]
The distance of the centre of mass from the side BC is \[{d_{BC}} = \dfrac{4}{3}\]
The equation of the line AC is,
\[y - 4 = \dfrac{{0 - 4}}{{3 - 0}}\left( {x - 0} \right) \Rightarrow y = - \dfrac{4}{3}x + 4\]
So, the side AC is along \[4x + 3y - 12 = 0\]
The distance of the centre of mass from the side CA is,
\[{d_{CA}} = \left| {\dfrac{{\left( {4 \times 1} \right) + \left( {3 \times \dfrac{4}{3}} \right) - 12}}{{\sqrt {{4^2} + {3^2}} }}} \right|\]
\[\Rightarrow {d_{CA}} = \dfrac{4}{5}\]

Image: The right triangular plate in cartesian coordinate system.
The order of the distance of the centre of mass of the right triangular plate from the sides is as,
\[{d_{Bc}} > {d_{AB}} > {d_{CA}}\]
As the moment of inertia is proportional to the square of the distance of the centre of mass from the axis of rotation,
\[{I_2} > {I_1} > {I_3}\]
Hence, the statement \[{I_3} > {I_2}\] is incorrect.
Therefore,the correct option is (D).
Note: The moment of inertia about the smaller side of the triangular lamina is maximum because the effective distance of the centre of mass is from the axis of rotation is maximum.
Recently Updated Pages
Arithmetic, Geometric & Harmonic Progressions Explained

Cartesian Form of Vector Explained: Formula, Examples & Uses

Apparent Frequency Explained: Formula, Uses & Examples

Calorimetry: Definition, Principles & Calculations

Centrifugal Force Explained: Definition, Formula & Examples

Charge in a Magnetic Field: Definition, Formula & Examples

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Understanding Atomic Structure for Beginners




