Question

The volume vs. temperature graph of one mole of an ideal gas is given below:

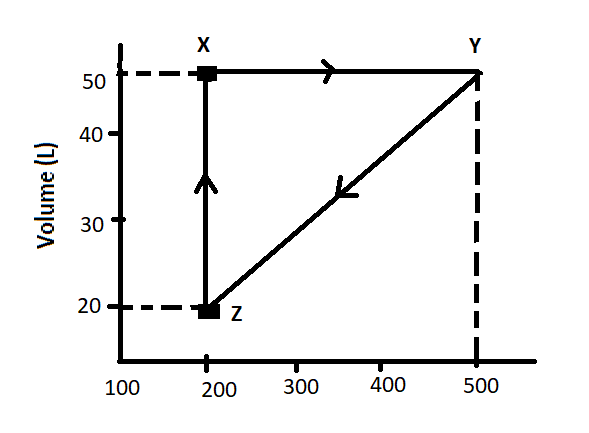
The pressure of the gas (in atm) at X, Y and Z respectively are:
[A] 0.328, 0.820, 0.820
[B] 3.28, 8.20, 3.28
[C] 0.238, 0.280, 0.280
[D] 32.8, 0.280, 82.0

Answer 1

Hint: To solve this question, use the ideal gas equation, PV = nRT. Find the volume and temperature for each gas using the given graph and use it to find the pressure at each of the give points X, Y and Z. Remember to use the value of the gas constant in lit-atm/mol k.

Complete step by step solution: We know that the ideal gas equation is PV = nRT where P is the pressure, V is the volume of the gas, n is the number of moles, R is the universal gas constant which has a fixed value and T is the temperature.
We can use this ideal gas equation to find out the pressure. We can get the temperature and the volume from the above graph.

Let us calculate the pressure of the gas at X-
As we can see from the graph that volume in litre for X is 50L and temperature is 200 kelvin. In the question, it is mentioned that one mole of an ideal gas is used therefore we can write that n is 1. The value of R is known to us in atm which is 0.082 lit-atm/mol K.
Therefore, putting these values in the equation, we will get-
P$\times $ 50L = 1 mol $\times $ 0.082 lit atm/mol k $\times $ 200 k
Or, $P=\dfrac{1mol\times 0.082Latm/molK\times 200K}{50L}=0.328atm$

Therefore, the pressure of one mole of an ideal gas at X is 0.0328 atm.

Now, at position Y, as we can see from the graph that volume is 50L and temperature is 500K.
Therefore, putting these values in the ideal gas equation, we will get –
$P=\dfrac{1mol\times 0.082Latm/molK\times 500K}{50L}=0.82atm$

Therefore, the pressure of one mole of an ideal gas at Y is 0.082atm.

And lastly, at position Z, we have temperature 200K and volume 20L.
Therefore, from the ideal gas law equation, the pressure will be-
$P=\dfrac{1mol\times 0.082Latm/molK\times 200K}{20L}=0.82atm$

The pressure of the ideal gas at Z is 0.82atm.

As we can see from the above discussion that pressure of one mole of the ideal gas at X, Y and Z is 0.328atm, 0.82atm and 0.82atm respectively.

Therefore, the correct answer is option [A] 0.328, 0.820, 0.820.

Note: The ideal gas law equation is an equation of state variables of a hypothetical ideal gas. It has many limitations but still used for approximation of the behaviour of a gas under certain conditions. It is a combination of Boyle’s law, Avogadro’s law, Charles’s law and Gay-Lussac’s law. However, this equation does not help us to understand whether a gas heats or cools during expansion or compression.