Question

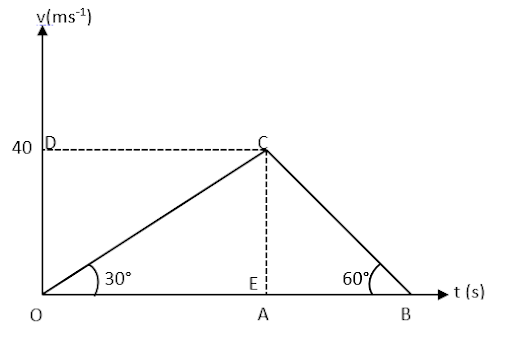
The velocity-time graph of a body is shown in Figure mentioned below. The ratio of average acceleration during the intervals OA and AB is
A. 1
B. \[\dfrac{1}{2}\]
C. \[\dfrac{1}{3}\]
D. 3

Answer 1

Hint: The slope of the velocity-time graph of a body is the rate of change of velocity. As we know that the rate of change of velocity is equal to the acceleration of the body. Hence, the acceleration of the body is the slope of the velocity-time graph.

Formula used:
\[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\],
Here, m is the slope of the line joining two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\].
\[m = \tan \theta \]
Here m is the slope of the line making an angle of \[\theta \] with the horizontal.

Complete step by step solution:
Initially the body is at rest, i.e. at \[t = 0s\]the velocity of the body is \[{v_0} = 0.0\,m/s\]. For the part of OA, the slope of the velocity-time graph is constant and the line is making an angle of 30° with the axis which represents time. So, the acceleration for the motion in part OA will be the tangent of angle 30°.

Let the acceleration of the body in part OA is \[{a_{OA}}\], then
\[{a_{OA}} = \tan 30^\circ \]
\[\Rightarrow {a_{OA}} = \dfrac{1}{{\sqrt 3 }}m{s^{ - 2}}\]
For the part of AB, the slope of the velocity-time graph is constant and the line is making an angle of 60° with the axis which represents time. So, the acceleration for the motion in part AB will be the tangent of angle 30°

Let the acceleration of the body in part AB is \[{a_{AB}}\], then
\[{a_{AB}} = \tan 60^\circ \]
\[\Rightarrow {a_{AB}} = \sqrt 3 m{s^{ - 2}}\]
We need to find the ratio of the acceleration in the interval OA to the acceleration in the interval AB,
\[\dfrac{{{a_{OA}}}}{{{a_{AB}}}} = \dfrac{{\left( {\dfrac{1}{{\sqrt 3 }}} \right)m{s^{ - 2}}}}{{\sqrt 3 m{s^{ - 2}}}}\]
\[\Rightarrow \dfrac{{{a_{OA}}}}{{{a_{AB}}}} = \dfrac{1}{{\sqrt 3 \times \sqrt 3 }}\]
\[\therefore \dfrac{{{a_{OA}}}}{{{a_{AB}}}} = \dfrac{1}{3}\]

Therefore, the correct option is A.

Note: Ratio is the pure number, i.e. it is dimensionless quantity. The acceleration is the vector quantity which is having magnitude as well as direction. To find the magnitude we take the acute angle made by the velocity-time graph with the horizontal axis.