Question

The temperature of the water of a pond is \[0{}^\circ C\] while that of the surrounding atmosphere is \[-20{}^\circ C\] . If the density of ice is \[\rho \] , the coefficient of thermal conductivity is \[\kappa \] and latent heat of melting is \[L\] then the thickness \[Z\] of the ice layer formed increases as a function of time \[t\] as:
(A) \[{{Z}^{2}}=\dfrac{60\kappa }{\rho L}t\]
(B) \[Z=\sqrt{\dfrac{40\kappa }{\rho L}t}\]
(C) \[{{Z}^{2}}=\dfrac{40\kappa }{\rho L}\sqrt{t}\]
(D) \[{{Z}^{2}}=\dfrac{40\kappa }{\rho L}t\]

Answer 1

Hint: The heat required for the ice layer to be formed will be the latent heat of fusion and it will be provided by the surrounding atmosphere. Since ice formation always occurs in layers, we will begin our solution by taking a thin ice layer of a certain area. This area will be an effective area for heat transaction between the ice layer and the surroundings. Basically the ice will lose heat to the surrounding.

Formula Used:
\[Q=mL\]
\[\dfrac{Q}{t}=\dfrac{\kappa A({{T}_{2}}-{{T}_{1}})}{d}\]

Complete step by step answer:

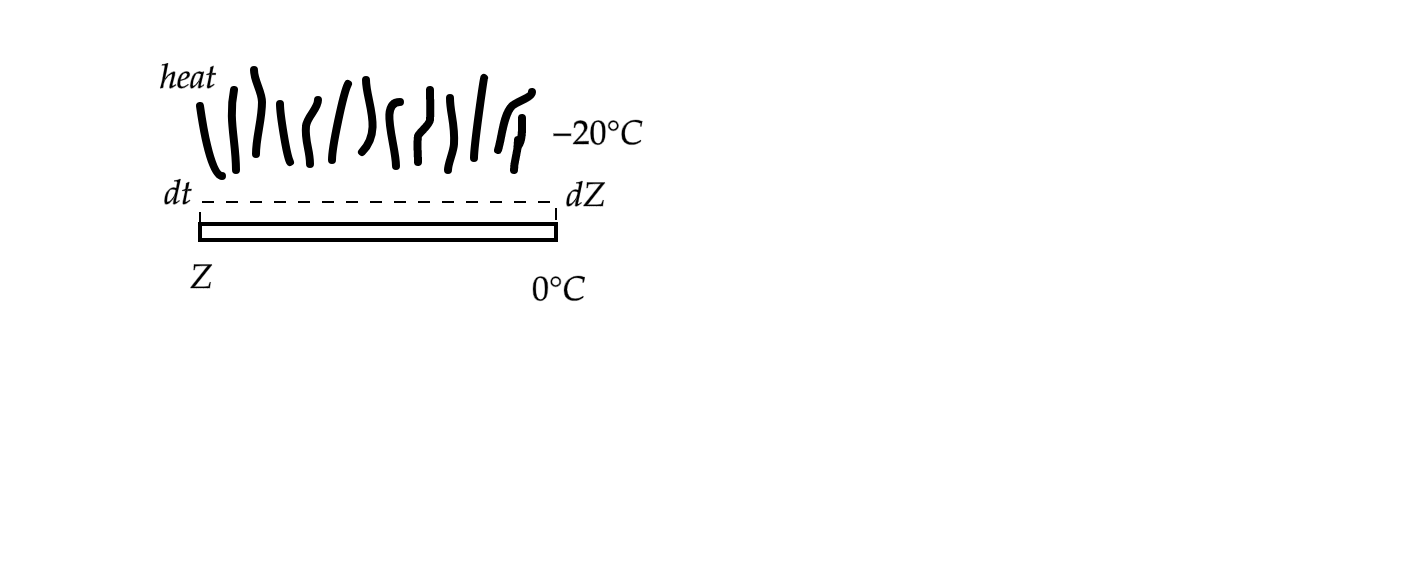
Let the thickness of the ice layer at \[t=0\] being \[Z\] and the effective area of heat exchange being \[A\]
In time \[dt\] , the thickness of the ice layer increases by \[dZ\] (say)
The heat required for ice layer formation is given as,
\[\begin{align}
  & Q=mL \\
 & \Rightarrow Q=(\rho \times V)\times L \\
 & \Rightarrow Q=\rho \times (A\times dZ)\times L \\
\end{align}\]
Now, heat change in the surrounding is given as,
\[Q'=\dfrac{\kappa \times A\times \Delta T}{Z}dt\] where the other symbols have meanings as stated in the question and \[\Delta T\] are the temperature difference.
Since the heat change in the surrounding is the heat responsible for ice layer formation, we can say that \[Q=Q'\]
Substituting the values, we get \[\rho \times (A\times dZ)\times L=\dfrac{\kappa \times A\times \Delta T}{Z}dt\]
Since the area is a common factor on both sides, we can cancel it out.
Rearranging the terms, we get \[ZdZ=\dfrac{\kappa \Delta T}{\rho L}dt\]
The temperature difference between the ice layer and the surroundings \[(\Delta T)=0-(-20)=20{}^\circ C\]
Substituting the values in the expression, we get \[ZdZ=\dfrac{20\kappa }{\rho L}dt\]
Integrating both sides, we have
\[\begin{align}
  & \int{ZdZ}=\int{\dfrac{20\kappa }{\rho L}dt} \\
 & \Rightarrow \dfrac{{{Z}^{2}}}{2}=\dfrac{20\kappa }{\rho L}t+c \\
 & \Rightarrow {{Z}^{2}}=\dfrac{40\kappa }{\rho L}t+c \\
\end{align}\]
Since we just have to establish a relation between the thickness of the ice and the time, we can leave out the constant of integration and say that \[{{Z}^{2}}=\dfrac{40\kappa }{\rho L}t\] .

Hence option (D) is the correct answer.

Note: Sometimes we have to assume quantities which are not provided in the equation but are needed for our solution, for example, in this question, the effective surface area for heat exchange was not mentioned so we assumed it to have a certain value. Most of the time, these assumed values get cancelled at some step of the solution but if they don’t, they can easily be expressed in terms of quantities known to us.