Question

The system shown is just on the verge of slipping. The coefficient of static friction between the block and the tabletop is

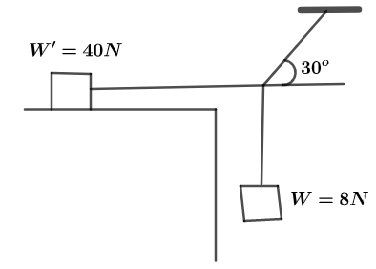
(A) $0.5$
(B) $0.95$
(C) $0.15$
(D) $0.35$

Answer 1

Hint: In order to solve this question, we will first draw the free diagram with all the forces acting on the blocks and string of the system and then by applying the forces equilibrium condition, we will solve for the coefficient of static friction between the block and tabletop.

Complete answer:
Let us first draw the free diagram of the system with all the forces acting on the system as

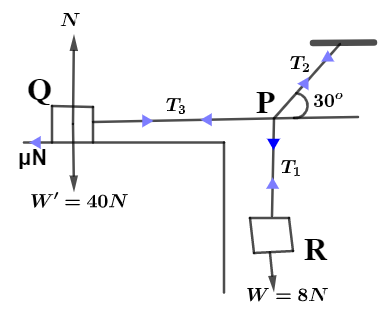
where, N is the normal force for block Q, ${T_1},{T_2},{T_3}$ be the Tension force acting on the strings and $\mu N$ be the static frictional force between block Q and tabletop. Now,
For equilibrium of block R we have,
${T_1} = W = 8N$

Equilibrium at point P, the vertical component of ${T_2}$ is equal to ${T_1}$ so, we have
${T_2}\sin {30^o} = {T_1}$
on putting the values, we get
$
  {T_2}\dfrac{1}{2} = 8 \\
  {T_2} = 16N \\
 $

Now, the horizontal component of ${T_2}$ is equal to ${T_3}$ so, equilibrium for block Q is
${T_2}\cos {30^o} = {T_3}$
on putting the values, we get
$
  (16)\dfrac{{\sqrt 3 }}{2} = {T_3} \\
  {T_3} = 8\sqrt 3 N \\
 $

Now, normal reaction force on block Q is $N = W' = 40N$ and the static frictional force is balanced by the tension ${T_3} = \mu N$
so, on putting the values we get
$
  8\sqrt 3 = \mu (40) \\
  \mu = \dfrac{{\sqrt 3 }}{5} \\
  \mu = 0.35 \\
 $
So, the coefficient of static friction between tabletop and block is $\mu = 0.35$

Hence, the correct answer is option (D) $0.35$

Note: It should be remembered that, basic trigonometric values must be known which are used here as
$
  \sin {30^o} = \dfrac{1}{2} \\
  \cos {30^o} = \dfrac{{\sqrt 3 }}{2} \\
 $
And always draw the free diagram with all necessary forces acting on the system with their direction to solve such problems.