Question

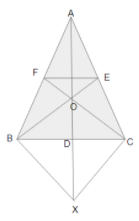
The side \[{\text{BC}}\] of a triangle \[{\text{ABC}}\] is bisected at \[{\text{D}}\]; \[{\text{O}}\] is any point in \[{\text{AD}}\]. \[{\text{BO}}\] and \[{\text{CO}}\] produced to meet \[{\text{AC}}\] and \[{\text{AB}}\] in \[{\text{E}}\] and \[{\text{F}}\] respectively and \[{\text{AD}}\] is produced to \[{\text{X}}\] so that \[{\text{D}}\] is the midpoint of \[{\text{OX}}\]. Prove that \[{\text{AO:AX = AF:AB}}\] and show that \[{\text{EF}}\] is parallel to \[{\text{BC}}\].

Answer 1

Hint— The quadrilateral \[{\text{BOCX}}\] represents a parallelogram as the diagonals \[{\text{OX}}\] and \[{\text{BC}}\] intersects each other. So use the definition of a parallelogram which states that the opposite sides of a parallelogram are parallel to each other as \[{\text{D}}\] is the midpoint of the line \[{\text{BC}}\] which divides the line into two parts equally.

Complete step-by-step solution
We are given in the question that the side \[{\text{BC}}\] of a triangle \[{\text{ABC}}\] is bisected at \[{\text{D}}\]; \[{\text{O}}\] is any point in \[{\text{AD}}\]. \[{\text{BO}}\] and \[{\text{CO}}\] are produced to meet \[{\text{AC}}\] and \[{\text{AB}}\] in \[{\text{E}}\] and \[{\text{F}}\] respectively and \[{\text{AD}}\] is produced to \[{\text{X}}\] so that \[{\text{D}}\] is the midpoint of \[{\text{OX}}\].
There are two objectives that need to be fulfilled. First is to prove that \[{\text{AO:AX = AF:AB}}\] and secondly we need to show that \[{\text{EF}}\] is parallel to \[{\text{BC}}\].
Consider the first objective,
As from the figure it is clear that, in a quadrilateral \[{\text{BOCX}}\] \[{\text{BD = DC}}\] and \[{\text{DO = DX}}\] as \[{\text{D}}\] is the midpoint of the line \[{\text{BC}}\] and \[{\text{OX}}\].
Since, the diagonals \[{\text{OX}}\] and \[{\text{BC}}\] of a quadrilateral \[{\text{BOCX}}\] intersects each other at \[{\text{D}}\].
Therefore, the quadrilateral \[{\text{BOCX}}\] becomes the parallelogram \[{\text{BOCX}}\].
Further, use the definition of parallelogram, which states that the opposite sides of a parallelogram are parallel to each other.
Thus, we get that,
\[{\text{BX||CO}}\] and \[{\text{CX||BO}}\]
Or \[{\text{BX||CF}}\] and \[{\text{CX||BE}}\]
Or \[{\text{BX||OF}}\] and \[{\text{CX||OE}}\]
Now, since \[{\text{BX||OF}}\] in the \[\Delta {\text{ABX}}\],
We get, \[\dfrac{{{\text{AO}}}}{{{\text{AX}}}} = \dfrac{{{\text{AF}}}}{{{\text{AB}}}}\]
Thus, from equation (1) we can conclude that \[{\text{AO:AX = AF:AB}}\]
Consider the second objective,
From above solution we have, \[\dfrac{{{\text{AO}}}}{{{\text{AX}}}} = \dfrac{{{\text{AF}}}}{{{\text{AB}}}}\] ---(1)
Next, we have \[{\text{CX||OE}}\] in the \[\Delta {\text{ACX}}\],
Thus, we get, \[\dfrac{{{\text{AO}}}}{{{\text{AX}}}} = \dfrac{{{\text{AE}}}}{{{\text{AC}}}}\] ---(2)
Consider the equations (1) and (2),
We get that,
\[\dfrac{{{\text{AF}}}}{{{\text{AB}}}} = \dfrac{{{\text{AE}}}}{{{\text{AC}}}}\]
Thus, we can conclude that as the points \[{\text{E}}\] and \[{\text{F}}\] divides the lines \[{\text{AB}}\] and \[{\text{AC}}\] respectively in the same ratio, so, \[{\text{FE||BC}}\].
Note: Do not forget to use the fact that as the diagonals of a quadrilateral bisect each other then the quadrilateral becomes the parallelogram and as the lines are parallel to each other, we can determine the ratio between the lines as the particular point cuts them. The midpoint divides the line into exactly two parts and both the parts are of equal length. When the points divide the lines in the same ratio then the lines are parallel to each other as shown.