
The lengths of the sides of a triangle is \[{\text{5 }}m\], \[1.2\] decameter and \[130{\text{ }}dm\]. Then its area is _______.
A. \[24{\text{ }}{m^2}\]
B. \[30{\text{ }}{m^2}\]
C. \[48{\text{ }}{m^2}\]
D. \[40{\text{ }}{m^2}\]
Answer
233.1k+ views
Hint: First of all, convert the lengths of sides of the triangle in meters. Now, use the formula, area of triangle \[ = \dfrac{1}{2} \times b \times h\] where \[b\] is the base of triangle and \[h\] is the height of the triangle in meters.
Complete step-by-step solution
Here, we have to find the area of the triangle having lengths of sides equal to 5m, \[1.2\] decameter and \[130{\text{ }}dm\].
We know that 1 decameter is \[10{\text{ }}m\] and \[{\text{1 }}dm = 0.1{\text{ }}m\]. Therefore, \[1.2\] decameter \[ = 1.2 \times 10 = 12{\text{ }}m\] and \[130{\text{ }}dm = 130 \times 0.1 = 13{\text{ }}m\].
So, the lengths of sides of the triangle in meters are \[{\text{5 }}m\], \[{\text{12 }}m\] and \[{\text{13 }}m\]. Let AB is \[{\text{5 }}m\], BC is \[{\text{12 }}m\] and CA is \[{\text{13 }}m\]. Then we can say that this triangle is a right-angled triangle because\[A{B^2} + B{C^2} = A{C^2}\].
\[
A{B^2} + B{C^2} = A{C^2} \\
{\left( 5 \right)^2} + {\left( {12} \right)^2} = {\left( {13} \right)^2} \\
25 + 144 = 169 \\
169 = 169 \\
\]
We know that the area of the triangle \[ = \dfrac{1}{2} \times b \times h\]…..(i) where \[b\] is the base of the triangle and \[h\] is the height of the triangle.
As we know that in a right angled triangle, the side with maximum length is hypotenuse. Therefore, CA is the hypotenuse of the triangle. We can take AB to be the height of the triangle and BC to be the base of the triangle.
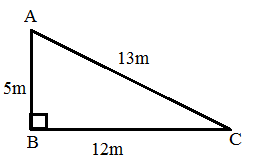
Height of the triangle \[h\] is \[{\text{5 }}m\].
Base of the triangle \[b\] is \[{\text{12 }}m\].
So, by substituting the value of \[h = {\text{5 }}m\]and \[b = {\text{12 }}m\] in equation (i), we get, area of triangle \[ = \dfrac{1}{2} \times b \times h\]
\[
= \dfrac{1}{2} \times 12 \times 5 \\
= 6 \times 5 \\
= 30{\text{ }}{m^2} \\
\]
So, we get the area of the triangle \[ = 30{m^2}\].
Therefore, the correct option is B.
Note: In this question, first of all, note that the units of length are different for all the sides. While calculating the area of a triangle all the length should be in the same unit. Also, identify the type of triangle before applying any formula because different types of triangles have different formulas to find area.
Complete step-by-step solution
Here, we have to find the area of the triangle having lengths of sides equal to 5m, \[1.2\] decameter and \[130{\text{ }}dm\].
We know that 1 decameter is \[10{\text{ }}m\] and \[{\text{1 }}dm = 0.1{\text{ }}m\]. Therefore, \[1.2\] decameter \[ = 1.2 \times 10 = 12{\text{ }}m\] and \[130{\text{ }}dm = 130 \times 0.1 = 13{\text{ }}m\].
So, the lengths of sides of the triangle in meters are \[{\text{5 }}m\], \[{\text{12 }}m\] and \[{\text{13 }}m\]. Let AB is \[{\text{5 }}m\], BC is \[{\text{12 }}m\] and CA is \[{\text{13 }}m\]. Then we can say that this triangle is a right-angled triangle because\[A{B^2} + B{C^2} = A{C^2}\].
\[
A{B^2} + B{C^2} = A{C^2} \\
{\left( 5 \right)^2} + {\left( {12} \right)^2} = {\left( {13} \right)^2} \\
25 + 144 = 169 \\
169 = 169 \\
\]
We know that the area of the triangle \[ = \dfrac{1}{2} \times b \times h\]…..(i) where \[b\] is the base of the triangle and \[h\] is the height of the triangle.
As we know that in a right angled triangle, the side with maximum length is hypotenuse. Therefore, CA is the hypotenuse of the triangle. We can take AB to be the height of the triangle and BC to be the base of the triangle.

Height of the triangle \[h\] is \[{\text{5 }}m\].
Base of the triangle \[b\] is \[{\text{12 }}m\].
So, by substituting the value of \[h = {\text{5 }}m\]and \[b = {\text{12 }}m\] in equation (i), we get, area of triangle \[ = \dfrac{1}{2} \times b \times h\]
\[
= \dfrac{1}{2} \times 12 \times 5 \\
= 6 \times 5 \\
= 30{\text{ }}{m^2} \\
\]
So, we get the area of the triangle \[ = 30{m^2}\].
Therefore, the correct option is B.
Note: In this question, first of all, note that the units of length are different for all the sides. While calculating the area of a triangle all the length should be in the same unit. Also, identify the type of triangle before applying any formula because different types of triangles have different formulas to find area.
Recently Updated Pages
Mutually Exclusive vs Independent Events: Key Differences Explained

Area vs Volume: Key Differences Explained for Students

Area of an Octagon Formula Explained Simply

Absolute Pressure Formula Explained: Key Equation & Examples

Central Angle of a Circle Formula Explained Quickly

Difference Between Vapor and Gas: JEE Main 2026

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Jan 21 Shift 1 Question Papers with Solutions & Answer Keys – Detailed Day 1 Analysis

JEE Main Response Sheet 2026 Released – Key Dates and Official Updates by NTA

JEE Main 2026 Answer Key OUT – Download Session 1 PDF, Response Sheet & Challenge Link

JEE Main Marks vs Percentile 2026: Calculate Percentile and Rank Using Marks

JEE Main 2026 Jan 22 Shift 1 Today Paper Live Analysis With Detailed Solutions

Other Pages
Pregnancy Week and Due Date Calculator: Find How Far Along You Are

NCERT Solutions For Class 10 Maths Chapter 11 Areas Related to Circles (2025-26)

NCERT Solutions For Class 10 Maths Chapter 12 Surface Areas and Volumes (2025-26)

All Mensuration Formulas with Examples and Quick Revision

Complete List of Class 10 Maths Formulas (Chapterwise)

NCERT Solutions for Class 10 Maths Chapter 13 Statistics




