
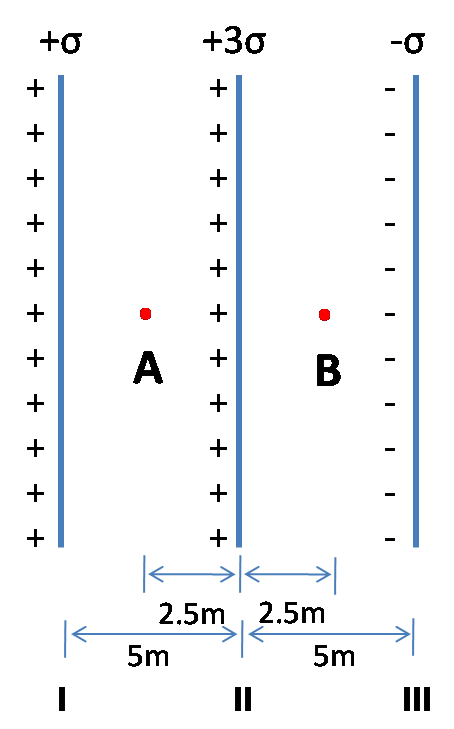
The figure shows three infinite non-conducting plates of charge perpendicular to the plane of the paper with charge per unit area \[ + \sigma , + 3\sigma \] and$ - \sigma $. The ratio of the net electric field at the point A to the point B is$1/x$ . Find x.
Answer
218.1k+ views
Hint: To solve this problem, first we need to find out the net electric fields at the points A and B. For that, we may use the equation for the electric field at a point near to an infinite non-conducting plate having a given charge density, $E = \dfrac{\sigma }{{2\varepsilon 0}}$. The net electric fields at both the points can be calculated by adding the individual electric fields due to each of the infinite non-conducting plates.
Formula used: Here we use the equation which can be derived from Gauss law: $E = \dfrac{\sigma }{{2\varepsilon 0}}$where $E$ is the electric field, $\sigma $ is the surface charge density or charge per unit area of the infinite non-conducting plate, and $\varepsilon 0$ is the permittivity of free space.
Complete step-by-step answer:
As we all can understand from the figure, it is clear that the net electric field at point A has contributions of the fields due to the plates I, II and III. The figure clearly describes that the surface charge densities of the plates I, II and III are $ + \sigma , + 3\sigma $and $ - \sigma $ respectively. Now, the electric field at point A due to the plate I would be:
\[EA\left( I \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}}\]
Similarly, the electric field at A due to the plates II and II are:
\[
EA\left( {II} \right) = \dfrac{{3\sigma }}{{2\varepsilon 0}} \\
EA\left( {III} \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\
\]
respectively. Now, the net electric field at A is given by:
\[
EA = EA\left( I \right) + EA\left( {II} \right) + EA\left( {III} \right) \\
\Rightarrow EA = \dfrac{{ - \sigma }}{{2\varepsilon 0}} + \dfrac{{3\sigma }}{{2\varepsilon 0}} + \dfrac{{ - \sigma }}{{2\varepsilon 0}} = \dfrac{\sigma }{{2\varepsilon 0}} \\
\]
Similarly the electric fields at point B due to the three plates are given by:
\[
EB\left( I \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\
EB\left( {II} \right) = \dfrac{{ - 3\sigma }}{{2\varepsilon 0}}and \\
EB\left( {III} \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\
\]
Thus, the net electric field at the point B can be estimated as:
\[
EB = EB\left( I \right) + EB\left( {II} \right) + EB\left( {III} \right) \\
\Rightarrow EA = \dfrac{{ - \sigma }}{{2\varepsilon 0}} + \dfrac{{ - 3\sigma }}{{2\varepsilon 0}} + \dfrac{{ - \sigma }}{{2\varepsilon 0}} = \dfrac{{ - 5\sigma }}{{2\varepsilon 0}} \\
\]
Finally, the ratio of the net electric field at point A to that at point B
\[\left| {\dfrac{{EA}}{{EB}}} \right| = \dfrac{\sigma }{{2\varepsilon 0}} \div \dfrac{{5\sigma }}{{2\varepsilon 0}} = \dfrac{\sigma }{{2\varepsilon 0}} \times \dfrac{{2\varepsilon 0}}{{5\sigma }} = \dfrac{1}{5}\]
So, as we found that the ratio of the net electric fields at both the points is $\dfrac{1}{5}$, the value of $x = 5$.
Note: When we are performing the calculation of the individual electric fields at both the points due to each of the non-conducting plates, we may sometimes end up in making the mistake of putting a wrong polarity. So, it is important to keep in mind that the electric field lines travel away from the positive plates while they travel towards the negative plates, shown in the illustration below. If we give the polarity of the field at a point depending on the direction of the field lines and then do the summation, the problem can be solved very easily.

Formula used: Here we use the equation which can be derived from Gauss law: $E = \dfrac{\sigma }{{2\varepsilon 0}}$where $E$ is the electric field, $\sigma $ is the surface charge density or charge per unit area of the infinite non-conducting plate, and $\varepsilon 0$ is the permittivity of free space.
Complete step-by-step answer:
As we all can understand from the figure, it is clear that the net electric field at point A has contributions of the fields due to the plates I, II and III. The figure clearly describes that the surface charge densities of the plates I, II and III are $ + \sigma , + 3\sigma $and $ - \sigma $ respectively. Now, the electric field at point A due to the plate I would be:
\[EA\left( I \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}}\]
Similarly, the electric field at A due to the plates II and II are:
\[
EA\left( {II} \right) = \dfrac{{3\sigma }}{{2\varepsilon 0}} \\
EA\left( {III} \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\
\]
respectively. Now, the net electric field at A is given by:
\[
EA = EA\left( I \right) + EA\left( {II} \right) + EA\left( {III} \right) \\
\Rightarrow EA = \dfrac{{ - \sigma }}{{2\varepsilon 0}} + \dfrac{{3\sigma }}{{2\varepsilon 0}} + \dfrac{{ - \sigma }}{{2\varepsilon 0}} = \dfrac{\sigma }{{2\varepsilon 0}} \\
\]
Similarly the electric fields at point B due to the three plates are given by:
\[
EB\left( I \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\
EB\left( {II} \right) = \dfrac{{ - 3\sigma }}{{2\varepsilon 0}}and \\
EB\left( {III} \right) = \dfrac{{ - \sigma }}{{2\varepsilon 0}} \\
\]
Thus, the net electric field at the point B can be estimated as:
\[
EB = EB\left( I \right) + EB\left( {II} \right) + EB\left( {III} \right) \\
\Rightarrow EA = \dfrac{{ - \sigma }}{{2\varepsilon 0}} + \dfrac{{ - 3\sigma }}{{2\varepsilon 0}} + \dfrac{{ - \sigma }}{{2\varepsilon 0}} = \dfrac{{ - 5\sigma }}{{2\varepsilon 0}} \\
\]
Finally, the ratio of the net electric field at point A to that at point B
\[\left| {\dfrac{{EA}}{{EB}}} \right| = \dfrac{\sigma }{{2\varepsilon 0}} \div \dfrac{{5\sigma }}{{2\varepsilon 0}} = \dfrac{\sigma }{{2\varepsilon 0}} \times \dfrac{{2\varepsilon 0}}{{5\sigma }} = \dfrac{1}{5}\]
So, as we found that the ratio of the net electric fields at both the points is $\dfrac{1}{5}$, the value of $x = 5$.
Note: When we are performing the calculation of the individual electric fields at both the points due to each of the non-conducting plates, we may sometimes end up in making the mistake of putting a wrong polarity. So, it is important to keep in mind that the electric field lines travel away from the positive plates while they travel towards the negative plates, shown in the illustration below. If we give the polarity of the field at a point depending on the direction of the field lines and then do the summation, the problem can be solved very easily.

Recently Updated Pages
Young’s Double Slit Experiment Derivation Explained

Wheatstone Bridge Explained: Working, Formula & Uses

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding Average and RMS Value in Electrical Circuits




