Question

The degrees of freedom of a diatomic gas at normal temperature is:
A) $3$
B) $4$
C) $5$
D) $6$

Answer 1

Hint: The degrees of freedom is the change in the state of the physical system or of the motion exhibited by the particular molecule which is located in a particular space. It varies for the monatomic, diatomic and the triatomic molecules.

Complete step by step solution:
The movement of the particle in the three dimensional space constitutes the three degrees of freedom. In the diatomic molecule, the whole molecule exhibits three degrees of freedom due to its centre of mass and also has another three degrees of freedom. These diatomic sets have been decomposed mainly in terms of the translation, vibration and the rotation of the molecule.

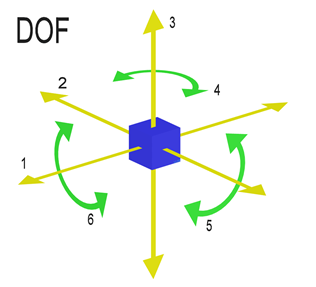
A single diatomic molecule has two rotational types of the motion and one vibrational type of the motion. In the diatomic molecule, the rotation takes place perpendicular to that of the axis joining the two atoms but it is not a physical degree of the rotation. Hence the degrees of freedom of the diatomic molecule is $6$ , but the vibration does not take place at the normal temperature. Hence the total number of the degree of freedom is calculated as follows.
$f = 3 + 2$
By adding the above degrees of freedom,
$f = 5$
Hence the degrees of freedom obtained for a diatomic gas molecule at a normal temperature is $5$ .

Thus the option (C) is correct.

Note: If the $N$ is the number of gas molecules in the container, hence the degrees of freedom is $f = 3N$ . If there occur any restrictions of the motion of the gas molecules and it is considered as $q$, then the degrees of freedom becomes $f = 3N - q$.