




How Does Orbital Velocity Keep Satellites in Orbit?
Orbital velocity refers to the minimum velocity a satellite requires to maintain a stable orbit around a planet or celestial body under gravity. This concept is foundational for understanding satellite motion, including the conditions for various orbits, and is critical in physics and engineering. Correct application of this concept is essential for analyzing satellite trajectories, their energy, and the forces acting upon them.
Orbital Velocity: Definition and Significance
Orbital velocity is defined as the speed that an object must attain so that the gravitational force from the central body provides exactly the centripetal force required for circular motion. For artificial satellites, this velocity ensures continued motion along a circular or elliptical path without the need for additional propulsion.
The value of orbital velocity depends on the mass of the central body and the radius of the orbit. For orbits closer to the planet, the required orbital velocity is higher due to the stronger gravitational force. These concepts are closely linked to the topic of Understanding Gravity.
Fundamental Equation for Orbital Velocity
The mathematical formula for orbital velocity is given by:
$v_o = \sqrt{\dfrac{GM}{r}}$
Here, $G$ represents the universal gravitational constant, $M$ is the mass of the central object, and $r$ is the radius of the orbit measured from the center of the attracting body. This formula demonstrates that orbital velocity does not depend on the mass of the satellite itself.
Orbital Motion and Forces Acting on Satellites
A satellite in circular orbit experiences two main forces: gravitational force and centripetal force. The gravitational attraction acts as the necessary centripetal force for the satellite to follow a circular trajectory. If either force changes, the orbital motion is altered.
At low altitudes, atmospheric drag can affect satellite motion by reducing speed and causing the satellite to descend. This is relevant to the study of Motion Of Satellites Of Earth.
Derivation: Expression for Orbital Velocity
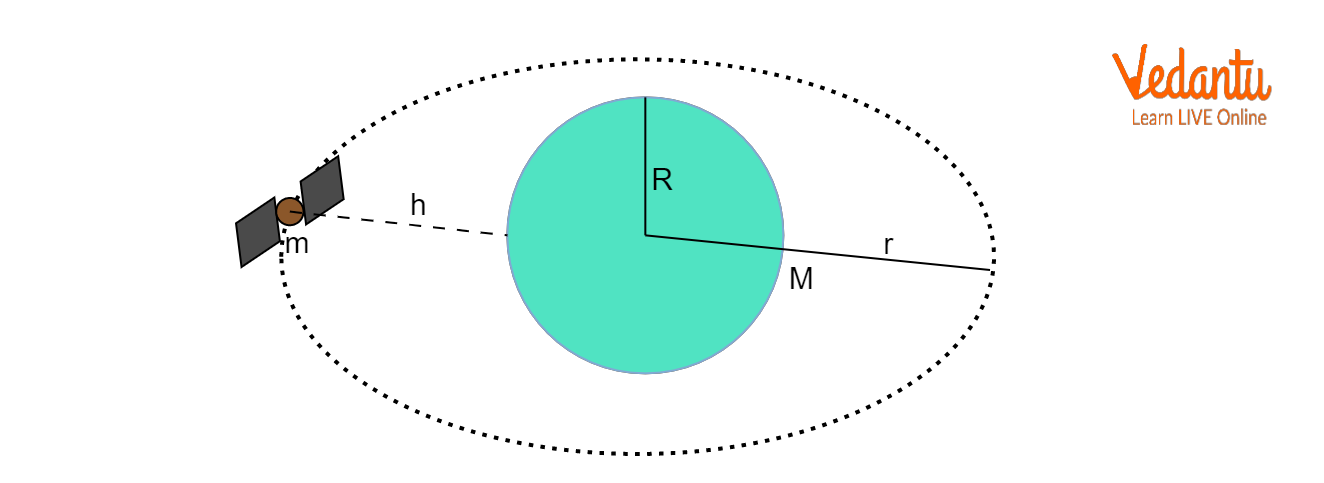
To derive the orbital velocity for a satellite of mass $m$ orbiting a planet of mass $M$ at radius $r$, equate the gravitational force to the required centripetal force:
$\dfrac{G M m}{r^2} = \dfrac{m v_o^2}{r}$
Solving for $v_o$ gives:
$v_o = \sqrt{\dfrac{GM}{r}}$
For a satellite at height $h$ above Earth's surface, $r = R + h$, where $R$ is the Earth's radius. Incorporating this, the velocity becomes:
$v_o = \sqrt{\dfrac{GM}{R + h}}$
Alternatively, since $GM = g R^2$ ($g$ is acceleration due to gravity), the expression can be written as:
$v_o = \sqrt{\dfrac{g R^2}{R + h}}$
Effects of Energy Loss on Satellite Orbits
If a satellite loses energy while in orbit, its orbital radius decreases, and the orbital velocity increases. The relationship between height and velocity shows that lower orbits require higher velocities. This principle is relevant for understanding changes in satellite trajectories due to frictional forces or deliberate maneuvers.
Such principles are also significant in topics like Gravitational Potential Energy, where potential and kinetic energies define satellite motion.
Typical Values: Orbital Velocity for Earth and Geostationary Satellites
The average orbital speed of Earth around the Sun is approximately $30\,\text{km/s}$. For satellites orbiting close to Earth's surface, the orbital velocity is about $7.9\,\text{km/s}$. Geostationary satellites, which orbit at an altitude of $35,786\,\text{km}$, have an orbital velocity of about $3.07\,\text{km/s}$.
| Parameter | Typical Value |
|---|---|
| Near Earth Orbital Velocity | $7.9\,\text{km/s}$ |
| Geostationary Orbit Velocity | $3.07\,\text{km/s}$ |
| Earth's Average Solar Orbit Velocity | $30\,\text{km/s}$ |
Application: Motion of Artificial and Natural Satellites
Both natural and artificial satellites require orbital velocity to maintain their orbits. The concept is independent of satellite mass, depending only on the mass of the central body and orbital radius. An understanding of nuclear forces within celestial objects is further expanded in Nuclear Structure And Composition.
For natural satellites such as the Moon, and artificial satellites used for communication or earth observation, precise calculation of orbital velocity is essential for stable functioning and desired coverage areas.
Key Points: Factors Affecting Orbital Velocity
- Mass of the central attracting body
- Radius of the satellite’s orbit
- Altitude above the planet’s surface
- Atmospheric drag at low altitudes
- Inertia of the orbiting body
- Gravitational acceleration at orbital height
Related Concepts in Orbital Motion
Orbital velocity is closely related to gravitational potential energy and kinetic energy, especially for circular and elliptical orbits. The total energy of a satellite in a stable orbit is the sum of its kinetic and potential energies, which determines the orbit type and stability. For further detail on kinetic energy in the context of molecular motion, reference Kinetic Energy And Molecular Speed.
Understanding these relationships forms the basis for advanced analysis of satellite dynamics in various gravitational fields and orbital configurations.
FAQs on Understanding Orbital Velocity and Satellite Motion
1. What is orbital velocity?
Orbital velocity is the minimum velocity an object must have to remain in stable orbit around a planet or celestial body due to gravitational force.
- It balances gravitational pull and centrifugal force.
- For Earth, near the surface, it is about 7.9 km/s.
- Determined by mass of planet and radius of orbit (v = √(GM/R)).
2. How do satellites stay in orbit around the Earth?
Satellites remain in orbit by moving at their orbital velocity, which creates enough centrifugal force to counteract gravitational pull.
- Gravity continuously pulls the satellite toward Earth.
- Its forward motion keeps it falling around the Earth, creating a stable orbit.
- Circular and elliptical orbits are both possible.
3. What is the formula for calculating orbital velocity?
The formula to calculate orbital velocity (v) is:
v = √(GM/R)
- G: universal gravitational constant
- M: mass of the central body (e.g., Earth)
- R: radius from the center of the mass to the orbiting object
4. Explain the difference between geostationary and polar satellites.
Geostationary satellites orbit above the equator with the same rotation period as the Earth, making them appear stationary.
Polar satellites move over the poles and scan the Earth as it rotates.
- Geostationary: Altitude ~36,000 km; used in communication and weather monitoring.
- Polar: Lower altitude (~500-800 km); used for remote sensing and Earth observation.
5. Why do satellites not fall back to Earth?
Satellites do not fall because their forward orbital velocity creates a force that balances Earth's gravity.
- They are continually ‘falling’ towards Earth, but their path curves with the planet.
- This balanced motion keeps them in stable orbit, instead of crashing down.
6. What is escape velocity and how is it different from orbital velocity?
Escape velocity is the minimum speed needed for an object to break free from a planet's gravitational pull, while orbital velocity is the speed required to stay in a stable orbit.
- Escape velocity is higher than orbital velocity.
- For Earth: escape velocity ~11.2 km/s; orbital velocity ~7.9 km/s (near surface).
- Escape velocity (vₑ) = √(2GM/R).
7. What factors affect the orbital velocity of a satellite?
The orbital velocity of a satellite depends mainly on:
- Mass of the central body (e.g., Earth).
- Radius/distance from the center of the central body to the satellite.
- Higher orbits require lower velocities due to decreased gravity.
8. What is the significance of geostationary satellites?
Geostationary satellites remain fixed above one location on Earth's equator, providing uninterrupted coverage.
- Ideal for television signals, communications, and weather forecasting.
- Allow continuous monitoring of specific regions.
9. How does gravitational force keep a satellite in orbit?
The gravitational force of the Earth acts as the centripetal force, continuously pulling satellites toward its center, resulting in circular or elliptical orbits.
- This keeps the satellite moving along a fixed path.
- Exact velocity ensures a perfect balance between gravitational pull and outward inertia.
10. Can satellites have elliptical orbits? If yes, how do they work?
Satellites can have both circular and elliptical orbits.
- In elliptical orbits, satellite speed is fastest at the closest point (perigee) and slowest at the farthest (apogee).
- Used for certain weather, communication, and scientific satellites.
11. What happens to the orbital velocity as the altitude of a satellite increases?
As altitude increases, the orbital velocity required to maintain a stable orbit around Earth decreases.
- This is because gravity is weaker farther from Earth's center.
- Satellites in higher orbits move slower than those close to Earth’s surface.
12. Why do polar satellites provide complete coverage of the Earth?
Polar satellites move from pole to pole, and as Earth rotates beneath them, they pass over different regions on each orbit.
- This allows them to scan the entire surface of the Earth over time.
- Commonly used for mapping, remote sensing, and Earth observation.
























