




How Is the Angle of Repose Measured and Used?
The angle of repose is a key concept in physics and engineering that describes the steepest angle at which a pile of granular material remains stable without slumping. Understanding the angle of repose is important for the analysis and design of storage, handling, and transportation systems for particulate materials in various applications.
Definition of Angle of Repose
The angle of repose is defined as the maximum angle with the horizontal at which a material, such as sand or grains, can be piled without slumping. When granular solids are allowed to accumulate to form a heap, the sides of the pile exhibit a characteristic angle with respect to the horizontal, which is termed the angle of repose.
The angle of repose depends on particle properties, including shape, size, and surface texture, as well as on environmental factors such as moisture content. It provides an empirical measure of the flowability and cohesiveness of bulk materials.
Physical Basis and Determination
The angle of repose arises due to interparticle friction and cohesion. The heap remains stable until gravitational force acting down the slope exceeds the frictional and cohesive resistance. The measurement can be performed using several experimental methods, including fixed-funnel, tilting box, and revolving cylinder setups.
In a typical experimental determination, material is poured onto a horizontal surface to form a conical pile. The angle formed at the slope between the pile surface and the horizontal base corresponds to the angle of repose.
Relation to Coefficient of Friction
The angle of repose ($\theta$) is directly related to the coefficient of static friction ($\mu$) between the particles. When a particle on the surface of the pile is at the threshold of sliding, the following relation holds:
$\mu = \tan \theta$
This equation is derived by equating the downslope component of gravitational force to the maximum frictional resistance.

Therefore, the coefficient of friction can be determined experimentally by measuring the angle of repose. This relationship is especially useful in problems involving inclined planes and particulate material flow. Relevant concepts such as the Difference Between Static And Dynamic Friction are also important in this context.
Factors Influencing Angle of Repose
The angle of repose shows considerable variation with a material’s physical properties and external conditions. Increased particle size, roughness, and irregular shapes generally lead to higher angles of repose due to greater interparticle friction. Higher moisture content can also increase cohesiveness and raise the angle.
- Material shape and surface texture
- Particle size distribution
- Moisture content of material
- Presence of fines or stickiness
- Filling method and vibration
Smooth, rounded grains tend to have lower angles of repose, indicating better flowability, while finely divided or sticky materials demonstrate higher angles due to increased cohesion and friction.
Types of Angle of Repose in Practice
Different conditions give rise to variations such as unconstrained filling angle, constrained filling angle, and emptying angle. The unconstrained angle is observed when material is poured in open space, while the constrained angle appears when the pile is formed within a container. The emptying angle may be higher in practice due to additional resistance as material flows from storage.
Engineering Applications
Knowledge of the angle of repose is critical in designing silos, hoppers, storage bins, and chutes for particulate material handling. It determines the slope of bin walls, the design of conveyor angles, and influences safe storage practices. The angle is used to calculate expected flow behavior and material handling requirements.
This property is widely applied in industries that involve grains, powders, minerals, and construction materials. Bulk storage and reliable flow require careful consideration of the angle of repose and related parameters such as internal friction and material density.
Typical Values for Common Materials
The angle of repose varies for different materials, reflecting their flow characteristics. Lower values indicate free-flowing behavior, while higher values point to cohesive or sticky nature.
| Material | Angle of Repose (Degrees) |
|---|---|
| Flax Seed | 21–25 |
| Corn (Maize) | 21 |
| Buckwheat | 25 |
| Peanut (unshelled) | 40 |
| Rice (Bran) | 45 |
| Soybean | 21–35 |
| Rapeseed/Canola | 45 |
| Wheat | 28 |
| Sorghum | 30–44 |
Empirical classification is used to assess material flow using the angle of repose. Angles up to 35° reflect free-flowing behavior, 35–45° indicate some cohesiveness, and angles above 55° indicate very high cohesiveness and poor flow.
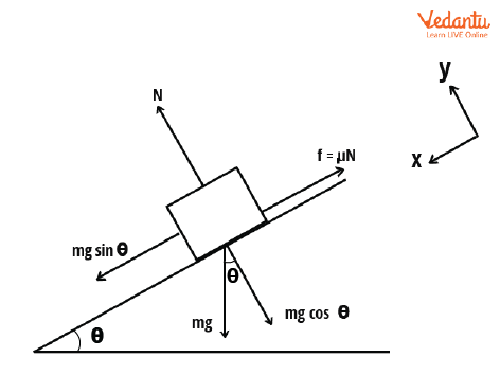
Examples and Sample Problem
A block of mass $m$ rests on a rough inclined plane. The block remains stationary as long as the inclination $\theta$ is less than the angle of repose. At the critical angle, the forces are balanced as shown below.
Normal force: $N = mg \cos \theta$
Frictional force at limiting value: $F = \mu N = mg \sin \theta$
At the angle of repose, set $mg \sin \theta = \mu mg \cos \theta$.
$\Rightarrow \mu = \tan \theta$
If the measured angle of repose for a powder is $37^\circ$, the coefficient of friction is $\mu = \tan 37^\circ \approx 0.75$.
The angle of repose is also useful in comparing the flowability of different materials. For detailed study of equilibrium and rotational motion, see Centre Of Mass and Moment Of Inertia.
Importance in Material Handling and Design
Proper understanding of the angle of repose helps engineers design storage bins and hoppers that minimize blockages and ensure continuous flow. The angle also determines the safe height and slope of bulk material piles in storage yards and silos.
The angle affects not only storage but also processes involving the movement of grains or powders under gravity, as seen in inclined conveyor belt design. For more on fundamental forces, refer to Force On A Current Carrying Conductor.
Relation to Other Physical Concepts
The angle of repose is conceptually related to the angle of friction, which is the angle between the resultant reaction and the normal to the surface when motion is impending. Both are governed by surface roughness and interparticle forces.
It also plays a role in understanding the balance of forces in inclined plane problems and is mathematically analogous to parameters used in Difference Between Mass And Weight analyses.
Summary of Key Points
- The angle of repose is the steepest stable angle for granular piles
- It is directly related to the coefficient of static friction
- Measurement of the angle provides information on material flow properties
- Used in the design and analysis of storage, handling, and conveying systems
- Typical values depend on material type and environmental conditions
A clear understanding of the angle of repose is essential for solving physics and engineering problems involving bulk materials. It is interconnected with other topics such as Work, Energy And Power in mechanical systems.
FAQs on Understanding the Angle of Repose
1. What is the angle of repose?
The angle of repose is the steepest angle at which a loose material remains stable without sliding. This concept is important in physics, geology, and engineering.
Key points:
- It is measured from the horizontal surface to the slope of the material.
- It depends on particle size, shape, moisture, and surface roughness.
- Commonly seen in piles of sand, soil, or grain.
2. What factors affect the angle of repose?
The angle of repose is influenced by several physical and chemical properties of materials.
Major factors include:
- Particle size – finer particles usually increase cohesion, altering the angle.
- Shape of particles – angular shapes increase interlocking, raising the angle.
- Moisture content – slight moisture increases cohesion; excessive moisture can reduce stability.
- Surface roughness – rougher surfaces increase friction, raising the angle.
3. How is the angle of repose measured?
To measure the angle of repose, a pile of material is formed and its slope is calculated with simple equipment.
Steps to measure:
- Pour dry granular material onto a flat surface to form a conical pile.
- Measure the height (h) and the radius (r) of the pile's base.
- Calculate: angle θ = arctan(h/r).
- Record the measurement for analysis or comparison.
4. Why is angle of repose important in engineering?
The angle of repose has critical engineering and construction applications, ensuring safety and efficiency.
Uses include:
- Designing stable slopes for embankments, dams, and embankments.
- Predicting stability in storage piles of materials like coal or grain.
- Avoiding landslides, avalanches, and material slippage.
- Optimising industrial equipment for material handling.
5. What is the difference between angle of repose and angle of friction?
Angle of repose and angle of friction both relate to stability, but describe different properties.
Key differences:
- Angle of repose: Maximum stable slope angle for loose material to remain at rest.
- Angle of friction: Minimum angle at which one body just starts to slide over another.
- Angle of repose is directly related to angle of internal friction for granular materials.
6. Can angle of repose change for the same material?
Yes, the angle of repose can vary for a single material based on different conditions.
Variation factors:
- Change in grain size (crushed vs. rounded grains)
- Variation in surface moisture or temperature
- Different deposition or pouring methods
7. What are practical examples of angle of repose in daily life?
The angle of repose can be observed in numerous everyday situations.
- Piling sand or soil into heaps
- Forming mounds of food grains or spices
- Construction and landscaping (e.g., slopes of hills or embankments)
- Industrial storage of powders and bulk solids
8. How does moisture affect the angle of repose of sand?
Increasing moisture in sand can significantly alter its angle of repose.
- Slight moisture increases cohesion and generally raises the angle, making the sand more stable.
- Excessive water decreases friction, lowering the angle and causing instability or slumping.
- Ideal moisture content creates the highest feasible angle of repose.
9. What is the typical angle of repose for dry sand?
The angle of repose for dry, loose sand typically ranges from 30° to 35°.
- It varies depending on grain shape and size.
- Clean, dry, rounded grains form the lowest angles.
- Angular or irregular grains result in higher angles.
10. Is angle of repose the same for all granular materials?
No, the angle of repose differs for each granular material depending on its properties.
Examples:
- Gravel: higher angle due to larger, angular particles
- Flour: lower angle, finer particles and less cohesion
- Bulk solids in industry will have variable angles based on particle type
























