Understanding the Polar and Euler Forms of Complex Numbers

A complex number admits representation in rectangular, polar, and exponential (Euler) forms. Each expresses the same quantity using distinct variables, supporting different operations and geometric interpretations.

Algebraic Definition and Notation for Polar Form of a Complex Number

Definition: The rectangular form of a complex number is $z = x + iy$, where $x$ is the real part and $y$ is the imaginary part. In polar form, $z$ is expressed using its modulus $r$ and argument $\theta$ as $z = r (\cos \theta + i \sin \theta)$.

The modulus $r$ equals $\sqrt{x^2 + y^2}$, and the argument $\theta$ is determined by $\theta = \tan^{-1} \left( \dfrac{y}{x} \right)$, with quadrant adjustments as required.

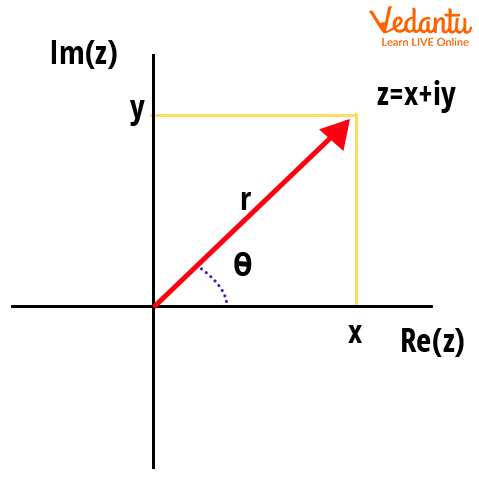
The Argand diagram illustrates the geometric interpretation, where $r$ is the distance from the origin and $\theta$ is the angle made with the positive real axis. For further reading, see Understanding Complex Numbers.

Calculation of Modulus and Argument in All Quadrants

If $z$ lies in the first or fourth quadrant, set $\theta = \tan^{-1} \left( \dfrac{y}{x} \right)$. In the second or third quadrant, use $\theta = \tan^{-1} \left( \dfrac{y}{x} \right) + \pi$ if $x < 0$.

Numerical calculations must be quadrant-aware to ensure the correct principal value for the argument. Reference: Modulus And Conjugate Of A Complex Number

Exponential (Euler) Form and Euler’s Identity

Result: Euler’s formula establishes $e^{i\theta} = \cos\theta + i\sin\theta$ for real $\theta$. The polar form $z = r (\cos \theta + i \sin \theta)$ is thus equivalent to the exponential form $z = r e^{i\theta}$.

This form is especially useful for multiplication, division, and finding powers or roots of complex numbers, due to properties of exponents. For direct algebraic forms, see Polar Form And Exponential Form.

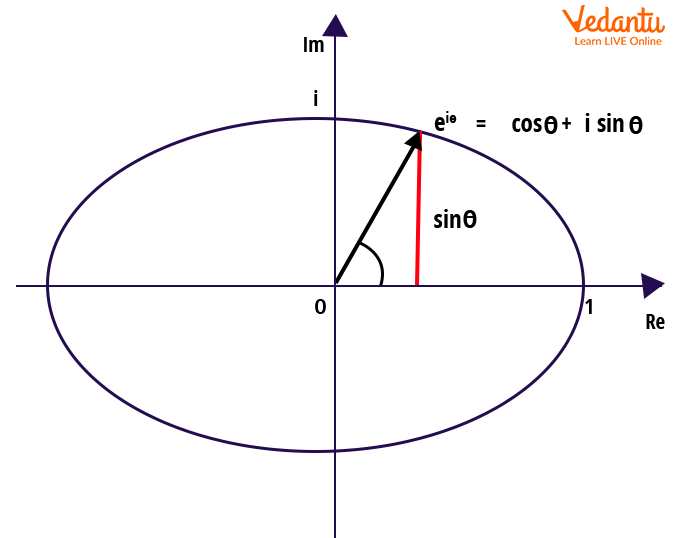
Power Series Justification of Euler’s Formula

Start from the real function power series: $e^{ix} = \sum_{n=0}^{\infty} \dfrac{(ix)^n}{n!}$. Expanding, group even and odd powers to obtain $e^{ix} = \cos x + i\sin x$ by comparing with the respective Maclaurin series.

Each component is justified by matching terms: real parts correspond to cosine series, imaginary parts to sine series. This underpins the equivalence of the polar and Euler forms.

Transformations: Cartesian, Polar, and Exponential Representations

To convert $z = x + iy$ to polar or Euler form, compute $r = \sqrt{x^2 + y^2}$ and $\theta = \tan^{-1}(y/x)$. Then $z = r (\cos \theta + i\sin \theta) = r e^{i\theta}$.

Conversely, to express $z = r e^{i\theta}$ in rectangular form, use $x = r \cos \theta$, $y = r \sin \theta$ for $z = x + iy$. For related transformations, see Polar And Eular Form.

Illustrative Calculations Using Euler and Polar Forms

Example: Evaluate $e^{i\pi/6}$.

Substitute $x = \pi/6$ in Euler’s identity: $e^{i\pi/6} = \cos(\pi/6) + i\sin(\pi/6)$.

$\cos(\pi/6) = \dfrac{\sqrt{3}}{2}$, $\sin(\pi/6) = \dfrac{1}{2}$.

Final result: $e^{i\pi/6} = \dfrac{\sqrt{3}}{2} + i \dfrac{1}{2}$.

Example: Convert $z = -3 + 3\sqrt{3}i$ to exponential form.

$r = \sqrt{(-3)^2 + (3\sqrt{3})^2} = \sqrt{9 + 27} = \sqrt{36} = 6$.

$\theta = \tan^{-1} \left(\dfrac{3\sqrt{3}}{-3}\right) = \tan^{-1}(-\sqrt{3})$. Since $x < 0$, add $\pi$ for a second-quadrant angle: $\theta = \frac{2\pi}{3}$.

Final result: $z = 6 e^{i\frac{2\pi}{3}}$.

Example: Find the product of $z_1 = 4 e^{i\frac{\pi}{4}}$ and $z_2 = 3 e^{i\frac{\pi}{6}}$.

Multiply moduli and add arguments: $z_1 z_2 = (4 \times 3) e^{i(\frac{\pi}{4} + \frac{\pi}{6})} = 12 e^{i\frac{5\pi}{12}}$.

For advanced usage, such as geometrical rotations and scaling, refer to Concept Of Rotation in Complex Numbers.

Notational Distinctions and Misconceptions in Polar and Exponential Forms

Common Error: Using incorrect argument branch in quadrant determination results in a wrong representation.

Carefully distinguish between argument range $(-\pi, \pi]$ and $[0, 2\pi)$ according to problem requirements. Maintain principal value consistency throughout calculations.

Typical JEE Patterns: Operations in Polar and Euler Forms

• Multiplication: moduli multiply, arguments add
• Division: moduli divide, arguments subtract
• Powers: moduli raised to power, arguments multiplied
• Roots: moduli rooted, multiple arguments spaced evenly

Mastering these rules streamlines solutions and avoids algebraic errors in exam applications. For polar-exponential manipulation, consult additional examples.