Question

In a triangle ABC, if vector BC=8, CA=7, AB=10, then find the projection of the vector AB on AC.
A.\[\dfrac{{25}}{4}\]
B. \[\dfrac{{85}}{{14}}\]
C. \[\dfrac{{127}}{{20}}\]
D. \[\dfrac{{115}}{{16}}\]

Answer 1

Hint: First draw the triangle with the given information, then apply the cosine law to find \[\cos A\].Then apply the projection formula to obtain the required solution.

Formula used
Cosine formula:
For a triangle ABC with sides a, b, c and A the angle between AB and AC then \[{a^2} = {b^2} + {c^2} - 2bc\cos A\].
The projection of the vector PQ on QR is \[PQ\cos Q\], where Q is the angle between PQ and QR.

Complete step by step solution
The diagram of the given problem is,

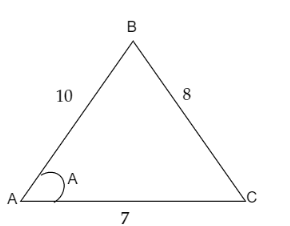
Image: Triangle ABC
Now, apply the cosine law,
\[{8^2} = {10^2} + {7^2} - 2 \times 10 \times 7\cos A\]
\[ \Rightarrow 2 \times 10 \times 7\cos A = {10^2} + {7^2} - {8^2}\]
\[\begin{array}{l} \Rightarrow \cos A = \dfrac{{{{10}^2} + {7^2} - {8^2}}}{{2 \times 10 \times 7}}\\{\rm{ = }}\dfrac{{85}}{{140}}\end{array}\]
Now, the projection of AB on AC is \[AB\cos A\] .
That is,
 \[\begin{array}{c}10\cos \left( {\dfrac{{85}}{{140}}} \right) = 10 \times \dfrac{{85}}{{140}}\\ = \dfrac{{85}}{{14}}\end{array}\]
Therefore the correct option is B.

Note: Students sometime confused with the fact that in triangle ABC what is the value of a, b, c. So, the side opposite to angle A is a, or we can say that the side that does not correspond to angle A is a, like this we can compute the values of b and c.