Question

If $P$ is any point within a $\Delta ABC$ , then $PA + CP$ is equal to
A. $AC + CB$
B. $BC + BA$
C. $CB + AB$
D. $CB + BA$

Answer 1

Hint: A triangle is a closed figure in a plane consisting of three segments called sides. Any two sides intersect at exactly one point called a vertex. A triangle can be classified according to its sides, angles or combination of both. Based on sides, we have: Equilateral triangle, Isosceles triangle and Scalene triangle having all three sides congruent, two sides congruent and no sides congruent respectively.

Complete step by step solution: 
We are given a $\Delta ABC$ with vertices $A$ , $B$ and $C$ .

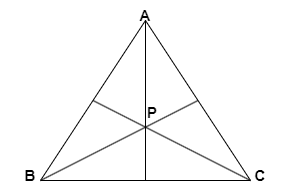
Image: Triangle ABC
Let two angle bisectors from vertex $A$ and $C$ , intersect at point $P$ .
Such that,
$CP + PA = CA$
Now using the property of the triangles, we have, “The Sum of lengths of two sides of a triangle $ \geqslant $ The length of the third side”. Here, we are considering it as equal.
We can write side $CA$ as the sum of other two sides, i.e.,
$CA = CB + BA$
Now, substituting the value of $CA$ in the above equation, we get
$CP + PA = CB + BA$
Hence, the correct option is D.

Note: All equilateral triangles are also isosceles triangles since every equilateral triangle has at least two of its sides congruent. Some isosceles triangles can be equilateral if all three sides are congruent. An angle bisector of a triangle is the segment that bisects an angle of a triangle. Every triangle has three angle bisectors.