Question

If earth were to spin faster, the acceleration due to gravity at the poles will:
(A) Increase
(B) Decrease
(C) Remains the same
(D) Cannot say

Answer 1

Hint If earth is spinning faster, this mean it has a higher angular velocity and thus a everyone on “off axis points” of earth will have a higher centrifugal force with respect to the axis of rotation of the earth

Complete step by step solution
When an object is placed on earth, it is constantly being pulled down due to gravity, this force is equal to mg. This is also the case when the earth is not rotating, if it was rotating then there would be another force which is also called the centrifugal force of the object. This force pushes the object from the surface of the earth and acts in the direction perpendicular to the axis of rotation of the earth. The net resultant of these 2 forces will give the apparent weight of the object


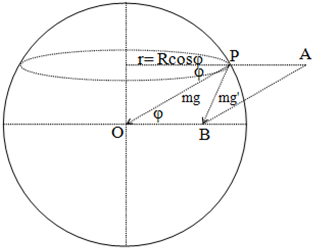
The resultant is thus given by,
 \[g'\, = \,g - {\omega ^2}R\cos \phi \]
At the equator \[\phi \] is equal to 0 and at the poles, \[\phi \] is equal to 90 which makes the 2nd term as 0. Therefore the acceleration due to gravity at the poles is independent of the angular velocity of the earth.

So the correct answer is option C.

Note Note that the weight of the body is the force they exert in the surface of Earth. This is higher on poles and lower on other points.
 If instead of pole, we need to take in consideration the gravity at the equator, it would be lower there. Also the angular velocity of earth under normal circumstances is \[7.29 \times {10^{ - 5}}\]