Question

Forces M and N acting at a point O make an angle \[{150^{^0}}\]. Their resultant acts at O have a magnitude 2 unit and are perpendicular to M. Then, in the same unit, find the magnitudes of M and N.
A. \[2\sqrt 3 ,4\]
B. \[\dfrac{{\sqrt 3 }}{2},2\]
C. 3,4
D. 4,5

Answer 1

Hint:Before we proceed with the problem, it is important to know about the resultant vectors. The overall force that acts on the object is called a resultant force. It is a single force. The forces should be vectors. The resultant force also tells in what direction it is acting on an object.

Formula Used:
The formula to find the resultant of a vector is given by,
\[\tan \varphi = \left( {\dfrac{{B\sin \theta }}{{A + B\cos \theta }}} \right)\]……………….. (1)
Where, \[\theta \] is angle between N and M.

Complete step by step solution:
Now we can solve the problem step by step as follows.

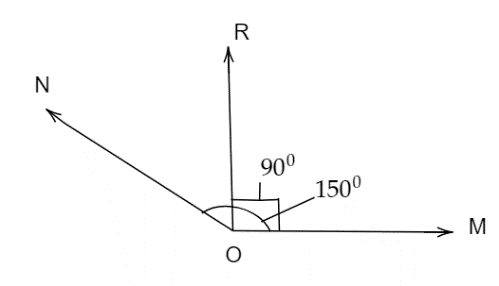
Image: Resultant vector of M and N

The resultant of 2 vectors will not be more than the sum of those 2 vectors, that is we can write it as,
Resultant vectors = sum of the two vectors
\[{2^2} = {\left( {M + N} \right)^2}\]
\[{2^2} = {M^2} + {N^2} + 2MN\cos \theta \]
Here, \[\theta \] is angle between N and M
\[{2^2} = {M^2} + {N^2} + 2MN\cos {150^0}\]
\[\Rightarrow 4 = {M^2} + {N^2} - \sqrt 3 MN\]………………… (2)
\[\Rightarrow \cos {150^0}\]can be written as, \[\cos \left( {{{180}^0} - {{30}^0}} \right) = \cos {30^0}\]

Now, considering the equation (1)
\[\tan \varphi = \left( {\dfrac{{B\sin \theta }}{{A + B\cos \theta }}} \right)\]
\[\Rightarrow \tan \left( {\dfrac{\pi }{2}} \right) = \left( {\dfrac{{N\sin {{150}^0}}}{{M + N\cos {{150}^0}}}} \right)\]
\[ \Rightarrow M + N\cos {150^0} = 0\]
\[ \Rightarrow M - N\left( {\dfrac{{\sqrt 3 }}{2}} \right) = 0\]
\[ \Rightarrow M = N\left( {\dfrac{{\sqrt 3 }}{2}} \right)\]………………….. (3)

Now, substituting the value of M in equation (2) we get,
\[4 = {\left( {N\dfrac{{\sqrt 3 }}{2}} \right)^2} + {N^2} - \sqrt 3 \left( {N\dfrac{{\sqrt 3 }}{2}} \right)N\]
\[\Rightarrow 4 = {N^2}\left( {\dfrac{1}{4}} \right)\]
\[\Rightarrow N = 4\]
In order to find the magnitude of M, substitute the value of N in equation (3) we get,
\[ \Rightarrow M = 4\left( {\dfrac{{\sqrt 3 }}{2}} \right)\]
\[ \Rightarrow M = 4\left( {\dfrac{{\sqrt 3 }}{2}} \right)\]
\[ \therefore M = 2\sqrt 3 \]
Therefore, the magnitudes of M and N are \[2\sqrt 3 ,4\].

Hence, option A is the correct answer

Note:Vectors are the units that have both magnitude and direction. We can immediately add and subtract if they are going in the same or the opposite direction. However, if they are all going in the same direction, we cannot just add. In a situation like this, we employ the resultant vector formula that will take the square root of each vector's sum of squares. The applications of resultant vectors are;
1. The Navigation boat is generally done using vectors.
2. Instructions of sports are based on using vectors.