




Kinetics
Chemical kinetics is the branch of physical chemistry that helps us to understand the rates of chemical reactions. The reaction can be classified as fast, moderate, or slow by studying the rate associated with it. Kinetics also allows us to analyze the effect of temperature, and catalyst on the rate of reaction and rate constant. It gives us information about mechanisms of reaction and allows us to assign specific rate constants to individual mechanistic steps.
Order of Reaction
Order of reaction refers to the relationship between the rate of reaction and the concentration of reactants taking part in a chemical reaction for example, in a first-order reaction the rate of reaction is directly proportional to the concentration of one reactant involved in the chemical reaction.
The order of reaction does not always depend on the stoichiometric coefficients in the balanced chemical equation. The sum of the power of concentration of reactants involved in reaction in the rate law expression is called the order of that chemical reaction.
The reaction can be zero, first or second order, and so on. The order of reaction can be an integer or fraction or zero. Methods to find an order of reaction are:-
Method of Initial Rates
The power-law equation is first converted to its natural logarithm form. It's calculated as $\ln r=\ln k+x \cdot \ln [A]+y \cdot \ln [B]+\ldots$
The partial order for each reactant is now estimated by running the reaction with different concentrations of the reactant in the issue while keeping the concentrations of the other reactants constant.
If the partial order of A is known, the rate equation's power-law expression becomes \ln$ \mathrm{r}=\mathrm{x} \cdot \ln [\mathrm{A}]+\mathrm{C}$, where C is a constant. The partial order, given by x, is plotted as a function of $\ln [A]$, and the corresponding slope is '$\ln r$' as a function of $\ln [A]$.
Integral Method
This method is commonly used to verify the order of reaction derived from the initial rates method. The integral form of the rate law is compared to the measured reactant concentrations.
For example, if the value of $\ln [A]$ corresponds to a linear function of time (integrated rate equation of a first-order reaction:
$\ln [A]-\ln \left[A_{0}\right]=-k t$, the rate law for a first-order reaction is verified.
Differential Method
This is the simplest method for determining the reaction order.
First, write the reaction's rate expression ($\mathrm{r}=\mathrm{k}[\mathrm{A}]^{\mathrm{x}}[\mathrm{B}]^{\mathrm{y}} \ldots$).
The final value of the reaction order is the sum of the exponents x+y+...
First Order Reaction
A first-order reaction is a chemical reaction in which the rate of reaction depends only on the concentration of one of the reactants. The order of the reaction is 1.
For a reaction $A\rightarrow B$
The rate of reaction can be defined as
$R=k[A]^t$
Where A is the concentration of reactant
This is an example of first-order reaction which gives the relationship of rate of reaction and reactant for first-order reaction.
Unit of rate constant for any order is given by
(mol L-1)1-ns-1
For first-order reaction n=1. The unit of rate constant for the first-order reaction will be s-1.
Examples
First-order reaction examples are:-
$\begin{align} &\mathrm{SO}_{2} \mathrm{Cl}_{2} \rightarrow \mathrm{SO}_{2}+\mathrm{Cl}_{2} \\ &2 \mathrm{H}_{2} \mathrm{O}_{2}(1) \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(1)+\mathrm{O}_{2}(\mathrm{~g}) \\ &\mathrm{N}_{2} \mathrm{O}_{5}(\mathrm{~s}) \rightarrow \mathrm{NO}_{2}(\mathrm{~g})+\mathrm{O}_{2}(\mathrm{~g}) \end{align}$
All nuclear reactions are first-order reactions. The number of radioactive atoms decaying per unit time in radioactive decay is proportional to the total number of radioactive atoms present at the time. Because the rate of decay is related to the first power of the number of radioactive atoms present, radioactive decay is first-order kinetics.
Rate Law for First-Order Reaction
For a reaction $A\rightarrow B$
The differential rate law for a first-order reaction is given as-
$\text { Rate }=-\dfrac{d a}{d t}=k[A]$
‘A’ is the concentration of reactant
‘K’ is the rate constant
The integral rate law is given by:
$\begin{align} &-\dfrac{\mathrm{da}}{\mathrm{dt}}=\mathrm{k}[\mathrm{A}] \\ &-\dfrac{\mathrm{da}}{\mathrm{A}}=k d t \\ &\int_{\left[\mathrm{A}_{\mathrm{e}}\right]}^{[\mathrm{A}]} \dfrac{d A}{A}=-\int_{t}^{t} k d t \end{align}$
First-order reaction formula
$\ln [A]-\ln \left[A_{0}\right]=-k t$
It can also be written as:
$\mathrm{A}=\mathrm{A}_{0} \ell^{-k t}$
Half Life of First Order Reaction
The half life time of reaction is defined as the time at which the concentration of reactant is half the initial concentration.
$\begin{align} &\mathrm{At}~\mathrm{t}=\dfrac{\mathrm{t}_{1}}{2} \mathrm{~A}=\dfrac{\mathrm{A}_{0}}{2} \\ &\dfrac{[\mathrm{A}]_{0}}{2}=[A]_{0} \ell^{-k t\dfrac{1}{2}} \end{align}$
Hence half life time for first-order reaction is given by
$t\dfrac{1}{2}=\dfrac{0.693}{k}$
Where k is the rate constant
Graphs
The first-order reaction graph between The concentration v/s time is given as:-

Graph for a first-order reaction
The graph for $\ln (A)$ v/s t for a first-order reaction is a straight line with slope -k The graph is a straight line with a negative slope which shows that the concentration of reactant decreases as the reaction proceeds.
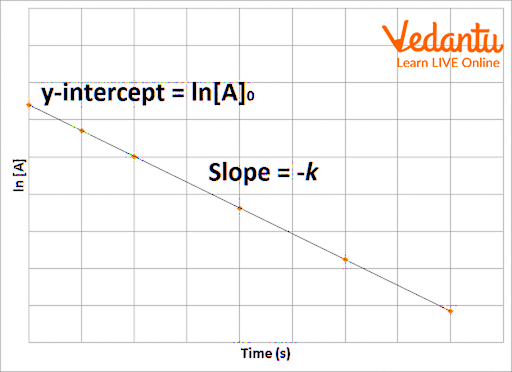
Graph shows the variation of logarithm of A wrt time
Summary
The kinetics of first-order reaction is the reaction in which the rate of reaction is directly proportional to the concentration of reaction. The order of the reaction is 1 hence called first-order reaction. Units of first-order reaction rate constant are given by s-1. The first order reaction equation is $\ln [A]-\ln \left[A_{0}\right]=-k t$. The graph for a first-order reaction between ln $\ln (A)$, and time is a straight line with a negative slope.
FAQs on First Order Kinetics for JEE
1. What is a pseudo first order reaction?
A Pseudo first order reaction can be defined as a second-order or bimolecular reaction that is made to behave like a first-order reaction. This reaction occurs when one reacting material is present in great excess or is maintained at a constant concentration compared with the other substance.
For example Hydrolysis of Cane Sugar
$\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}+\mathrm{H}_{2} \mathrm{O} \rightarrow \mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}+\mathrm{C}_{6} \mathrm{H}_{12} \mathrm{O}_{6}$
We can see that water has a very high concentration and so does not vary much during the reaction. As a result, the rate of the reaction is independent of the change in H2O concentration. The rate equation can be given as,
$\text { Rate }=\mathrm{k}\left[\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}\right]$
2. What is the molecularity of a reaction?
The molecularity of a reaction is defined as the number of molecules which collide simultaneously to bring about a chemical change. The molecularity of an elementary reaction is defined as the number of reactant molecules taking part in the reaction. It depends on the stoichiometric coefficient involved in a balanced chemical reaction.
Molecularity cannot be in fractions and cannot be negative.
For example
$2HI\rightarrow H_2+I_2$
In chemical reactions, the order and molecularity of a complex reaction are the same, and the order with regard to each reactant is equal to its stoichiometric coefficient. The molecularity in this reaction is two.
3. What is the difference between first order and zero order kinetics?
The differences between first order and zero order kinetics is as follows-
While zero order kinetics refers to chemical reactions whose rate of reaction does not depend on the concentration of the reactant, first order kinetics describes chemical reactions whose rate of reaction depends on the molar concentration of one reactant.
For first order kinetics, the graph of reactant concentration v/s time is curved, but for zero order kinetics, the graph is linear.
In zero order kinetics, rate law only takes into account the rate constant. In rate law, reactant concentration is multiplied by the rate constant.
























