Question

Can two isothermal curves cut each other?
A. Never
B. Yes
C. They will cut when temperature is ${0^ \circ }C$
D. Yes, when the pressure is critical pressure

Answer 1

Hint: In an Isothermal process in a thermodynamic system, the temperature is constant and at a constant temperature, both the parameters pressure and volume vary with the different conditions of the system and surroundings hence, we will plot a $P - V$ graph for an isothermal change for two different temperatures to state the answer of this problem.

Complete step by step solution:
An isothermal process in thermodynamics is defined as the process during which the temperature $T$ of a system remains constant that’s why it is also referred to as a constant-temperature process.

In an Isothermal process, $T = \text{constant}$ and $\text{Change in Temperature} = \Delta T = 0$. Now let us draw a $P - V$ graph for an isothermal expansion of a gas at two different temperatures to have two isothermal curves as shown below: -


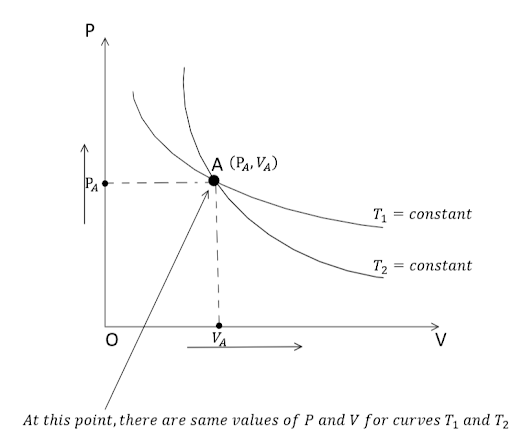
Clearly, from the above graph it can be observed that if the two isothermal curves intersect at point A, there will be the same values of pressure and volume i.e., ${P_A}$ and ${V_A}$ at that point. That’s why if the two curves intersect, the volume and pressure of the gas will be the same at two distinct isothermal temperatures, which is not possible. As a result, two isothermal curves can ‘Never’ intersect.

Hence, the correct option is A.

Note: In this problem, to determine whether the two isothermal curves intersect with each other or not, we need to find the conditions of other parameters of gas in a particular thermodynamic system such as pressure and volume hence, we will plot a $P - V$ graph and if the conditions of pressure and volume are justified for the given situation then the curves can intersect otherwise not.