Question

Assuming the coefficient of friction between the road and tires of a car to be 0.5, the maximum speed with which the car can move around a curve of 40.0m radius without slipping if the road is unbanked, should be
A. 25m/s
B. 19m/s
C. 14m/s
D. 11m/s

Answer 1

Hint: The practise of banking roads allows a car to travel around a curved track at a decent speed without skidding by lifting the outer edge of the curved road above the inner edge. To, solve this question we need to remember the concept of banking of road and the relation between the maximum velocity and coefficient of friction, which is given by ${{v}_{\max }}=\sqrt{\mu Rg}$

Formula used:
${{v}_{\max }}=\sqrt{\mu Rg}$
Where v is the velocity, R is the radius and $\mu $is the coefficient of friction and g is the acceleration due to gravity.

Complete answer:
We’ll start by equating all the forces and by trying to keep the body in equilibrium as shown in the diagram below:

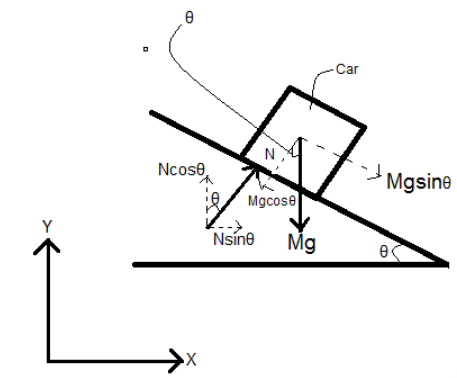
Let’s balance all the forces along the x axis
$f\cos \theta +N\sin \theta =\dfrac{m{{v}^{2}}}{R}$

We will now substitute $f=\mu N$ in the above equation we get,
$\mu N\cos \theta +N\sin \theta =\dfrac{m{{v}^{2}}}{R}$
$\mu (\cos \theta +\sin \theta )=\dfrac{m{{v}^{2}}}{R}$…….. (i)

Now similarly let’s balance all the forces along y axis
$N\cos \theta =f\sin \theta +mg$
$\Rightarrow N\cos \theta =\mu N\sin \theta +mg$
$\Rightarrow N(\cos \theta -\mu \sin \theta )=mg$…… (ii)

And frictional force Frictional force,$f=\mu N$.….. (iii)

Now we will divide the equation (i) by (ii), we get
$\dfrac{{{v}^{2}}}{Rg}=\dfrac{(\mu +\tan \theta )}{(1-\mu \tan \theta )}$
$\Rightarrow v=\sqrt{\dfrac{Rg(\mu +\tan \theta )}{(1-\mu \tan \theta )}}$.

For maximum velocity the road is unbanked,$\theta =0{}^\circ $
Therefore, ${{v}_{\max }}=\sqrt{\mu Rg}$

Now, in the given question we need to find v.
Given value of$R=40.0m$, $\mu =0.5$,$g=10m/{{s}^{2}}$.
Putting the value in ${{v}_{\max }}=\sqrt{\mu Rg}$.

We get,
$v=\sqrt{40\times 0.5\times 10}$
$\Rightarrow v=14.14m/s\approx 14m/s$

Hence, the correct option is C. 14m/s

Note: Students should fully grasp the idea of road banking because doing so will improve their ability to solve mechanical problems. Students should remember that prior knowledge of frictional force and centripetal force will help them better understand the idea of road banking.