Question

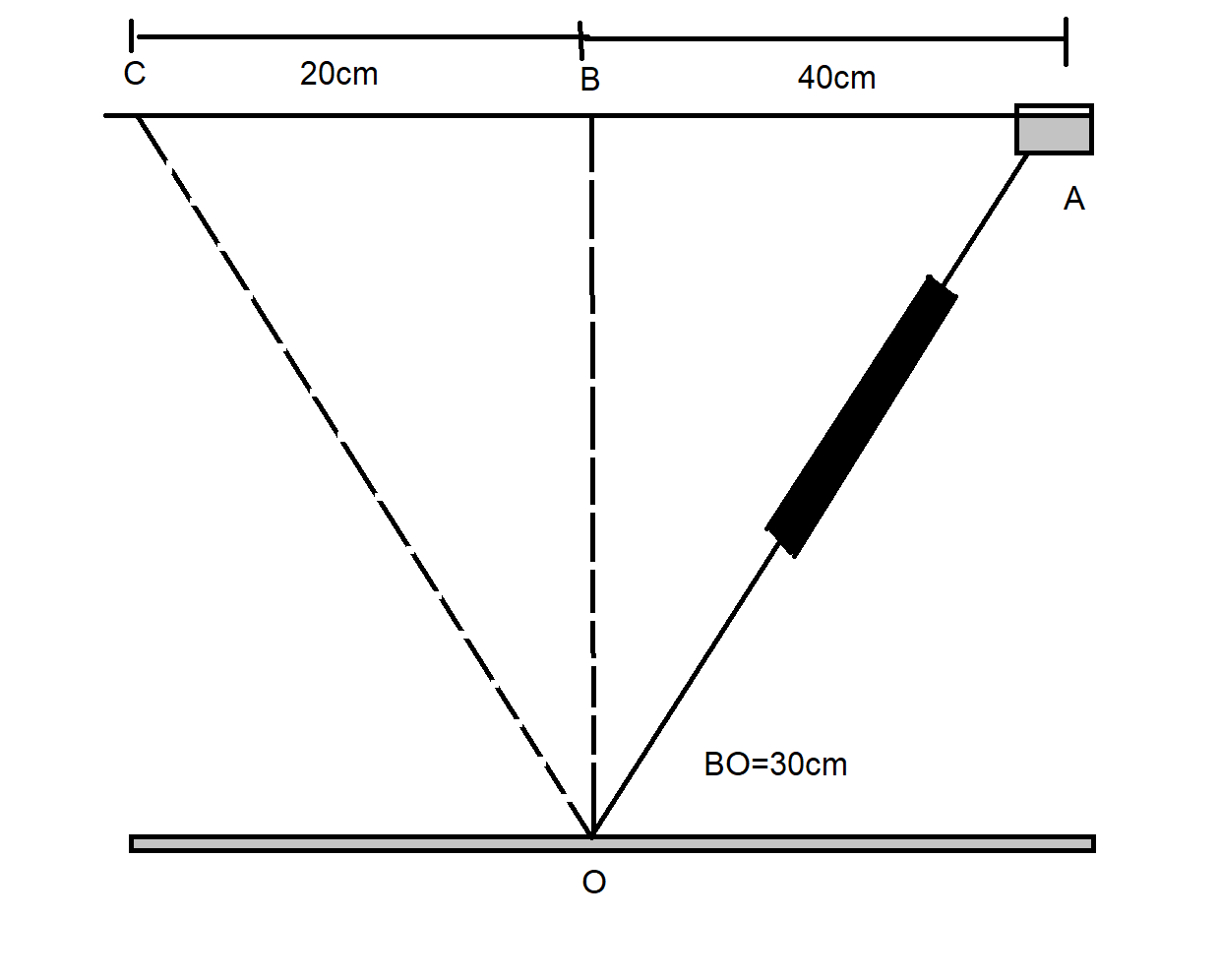
As shown in the figure, a smooth rod is mounted just above a table top. A$10kg$ collar, which is able to slide on the rod with negligible friction is fastened to a spring whose other end is attached to a pivot at $O$. The spring has negligible mass, a relaxed length of $10cm$ and a spring constant of $500N{m^{ - 1}}$. The collar is released from rest at point$A$.
(A) What is its velocity as it passes point $B$?
(B) Repeat for point $C$.

Answer 1

Hint We are given with a situation wherein a rod is sliding frictionless and are given with the spring constant and the relaxed or equilibrium position of the top and are asked to solve two problems. Thus, we will use the concept of conservation of energy for all the points. Thus, we will equate the formula for total energy for an oscillating body.
Formulae Used:
$E = T + U$
Where,$E$ is the total energy of the body,$T$ is the kinetic energy of the body and$U$ is the potential energy of the body.
$T = \dfrac{1}{2}m{v^2}$
Where,$m$ is the mass of the body and$v$ is the velocity of the body.
$U = \dfrac{1}{2}k{x^2}$
Where,$k$ is the spring constant of the spring and$x$ is the displacement of the body from its equilibrium position.

Complete Step By Step Answer
Here,
For point$B$,
${E_A} = {E_B}$
Further applying the formula, we get
${T_A} + {U_A} = {T_B} + {U_B}$
Now,
Applying the equations for the respective energy, we get
$\dfrac{1}{2}{m_A}{v_A}^2 + \dfrac{1}{2}k{x_A}^2 = \dfrac{1}{2}{m_B}{v_B}^2 + \dfrac{1}{2}k{x_B}^2$
Now,
As the point $A$ is the rest position, we have
${v_A} = 0$
${x_A} = OA - x$
${x_B} = BO - x$
Now,
$OA = \sqrt {{{(BO)}^2} + {{(AB)}^2}} $
Given,
$m = 10kg$
$x = 10cm$
$BO = 30cm$
And,
$AB = 40cm$
Thus,
Putting in the values, we get
$OA = \sqrt {{{\left( {30} \right)}^2} + {{\left( {40} \right)}^2}} $
Further, we get
$OA = \sqrt {900 + 1600} $
Then, we get
$OA = 50cm$
Now,
Substituting these values, we get
$\left( {500} \right){\left( {0.5 - 0.1} \right)^2} = \left( {10} \right){\left( {{v_B}} \right)^2} + \left( {500} \right){\left( {0.3 - 0.1} \right)^2}$
Further, we get
$80 = 10{\left( {{v_B}} \right)^2} + 20$
Then, we get
$60 = 10{\left( {{v_B}} \right)^2}$
After that, we get
${v_B}^2 = 6$
Then, we get
${v_B} = 2.45m{s^{ - 1}}$
Similarly,
For$C$,
${x_c} = OC - x$
Then,
$OC = \sqrt {{{\left( {20} \right)}^2} + {{\left( {30} \right)}^2}} $
Further, we get
$OC \approx 36cm$
Then,
$\left( {500} \right){\left( {0.5 - 0.1} \right)^2} = (10){({v_C})^2} + \left( {500} \right){\left( {0.36 - 0.1} \right)^2}$
Further, we get
$80 = 10{\left( {{v_C}} \right)^2} + 33.8$
Then, we get
$46.2 = 10{\left( {{v_C}} \right)^2}$
Then,
${v_C}^2 = 4.62$
Further, we get
${v_C} = 2.15m{s^{ - 1}}$
Hence, the answers are:
1. $2.45m{s^{ - 1}}$
2. $2.15m{s^{ - 1}}$

Note We have got the answers by applying the formulation of the energy conservation theorem. This is because, during the whole motion of the body, the only parameter which stays conserved is the energy of the body.