Question

As a body performs SHM, its potential energy U varies with time t as indicated in
A.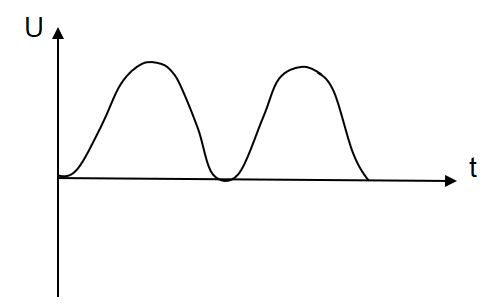
B.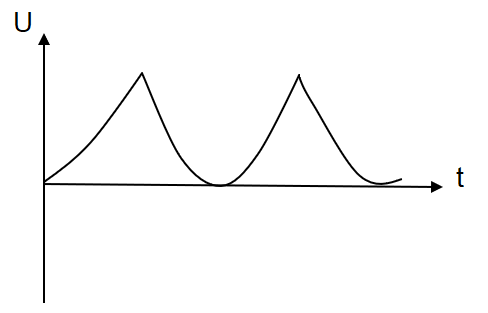
C.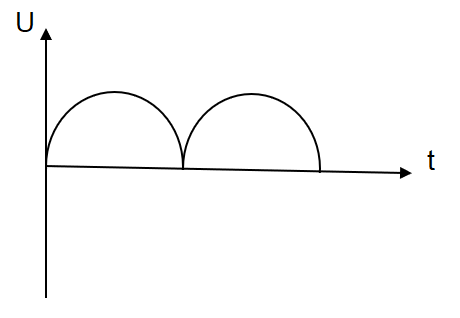
D.

Answer 1

Hint: Simple harmonic motion is defined as a periodic motion in which the acceleration(a) of a body is directly proportional to its displacement (x)and is directed towards the equilibrium position or mean position. The relation between the potential energy(U), kinetic energy(K), and time(t) in Simple Harmonic Motion or SHM at t = 0 can be obtained in a graph.

Formula used:
The potential energy (U) of a body performs SHM is given as:
\[U = \dfrac{1}{2}k{x^2}\] or \[U = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}\omega t\]
Where k is force constant
x is the displacement
m is mass of the particle
\[\omega \] is angular frequency
A is amplitude
t is time taken

Complete step by step solution:
As we know that potential energy U of a body performs SHM is,
\[U = \dfrac{1}{2}k{x^2}\]
As a body performs SHM, so we can write
\[x = A{\rm{ }}\sin \omega t\]
Now using this value in above equation, we have
\[U = \dfrac{1}{2}k{A^2}{\sin ^2}\omega t\]
Where \[\omega = \sqrt {\dfrac{k}{m}} \]
\[{\rm{ k = m}}{\omega ^2}\]
By using this value of k in above, we get
\[U = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}\omega t\]
So, by this equation we can see that at any time, t=0 then Potential energy will also become U=0. For any value of angle, it will always be positive. Hence a positive graph will be formed.

Hence option A is the correct answer.

Note: Simple Harmonic Motion or SHM can be defined as the motion in which the restoring force(F) is directly proportional to the displacement(x) of the body from its equilibrium or mean position. It is a special case of an oscillation in which the motion takes place in a straight line between the two extreme positions.