Question

An insect is at the bottom of a hemispherical ditch of radius 1 m. It crawls up the ditch but starts slipping after it is at height h from the bottom. If the coefficient of friction between the ground and the insect is 0.75, then h is ($g = 10\,ms^{-2}$)
A. 0.45 m
B. 0.60 m
C. 0.20 m
D. 0.80 m

Answer 1

Hint: In this question we will use the concept of friction force and normal force. We will balance the force at the point where slipping starts and then try to find the height of the point.

Formula used:
mgsin ϴ = µmgcos ϴ
where µ = coefficient of friction, m is the mass of the object, g is the acceleration due to gravity, and ϴ is the angle.

Complete step by step solution:
In the question let us consider the following diagram, where P= point where slipping starts, h= height of point P from the ground, O= bottom of the hemispherical ditch, O’= centre of the hemisphere lying on the axis perpendicular to the ground, ϴ= angle between PO’ and O’O and y=Radius - h

Now, we will balance the forces at point P. At point P, three forces are acting – Normal, friction and gravitational force. We will balance forces along the tangent at point P and perpendicular to it.


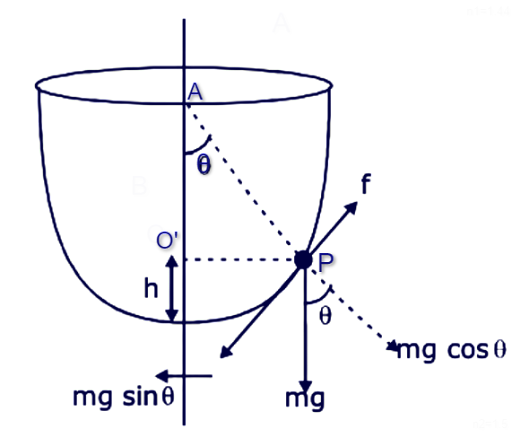
Along the tangent at point P:
mgsin ϴ = f(friction force)
$\Rightarrow $mgsin ϴ = µmgcos ϴ
where µ = coefficient of friction
$\Rightarrow \mu =\dfrac{mg\sin \theta }{mg\cos \theta }$
$\Rightarrow \mu =\tan \theta $
$\Rightarrow \tan \theta =0.75$, as given in the question
$\Rightarrow \tan \theta =\dfrac{3}{4}$
Now, $\tan \theta =\dfrac{perpendicular}{base}$
In a right-angled triangle with perpendicular = 3, base = 4, hypotenuse = 5 and ϴ=37°

Let the unknown vertex of the triangle formed with angle ϴ by A. Therefore, the triangle is O’AP. In triangle O’AP,
OAcos37°=y
$\Rightarrow \dfrac{4}{5}=y$
We know, y + h= R
$\Rightarrow \dfrac{4}{5}+h=1$
$\therefore $h = 0.20

Hence, the correct answer is option C.

Note: The surface reaction caused by the weight component is equivalent to the surface's normal reaction. Therefore normal reaction will cancel out the weight exerted perpendicular to the tangent at P since there is no motion.