Question

An ideal gas is taken through the cycle$A\to B\to C\to A$,$\Delta U$ as shown in the figure. If net heat supplied to the gas in the cycle is$5J$, the work done by the gas in the process$C\to A$ is:
(A) +5J
(B) +10J
(C) +15J
(D) +20J

Answer 1

Hint: By using the first law of thermodynamics find work done where net heat is $5J$. The first law of thermodynamics states that the change in internal energy of a system equals the net heat transfer into the system minus the net work done by the system. In equation form, the first law of thermodynamics: $\Delta U=q+W$.
Complete step by step answer:
The first law of thermodynamics is based on experience that energy can be neither created nor destroyed, if both the system and the surrounding are taken in account we can conclude it by saying energy is conserved.
Direct consequence of this statement is $U$ that is a state function. This implies that between any two fixed states ,there can be infinite processes or paths but $\Delta U$’ in all processes will remain the same $U$
Here as we know that the net heat applied in this process is$5J$.
Now returning to the initial point which is A, as we know Internal energy is a state function, which means that A is a constant before and after the cyclic process.
 Now according to first law of Thermodynamic
$\Delta U=q+W$
Here, $\Delta U$= Change in internal energy
              $q$=heat added
             $W$= work done
So we can say that
 $\Delta U=0$
 $q=-W$ OR \[W=-q\]
Now we can say that
${{W}_{A\to C}}={{W}_{A\to B}}+{{W}_{B\to C}}-q$ ……….(1)
      
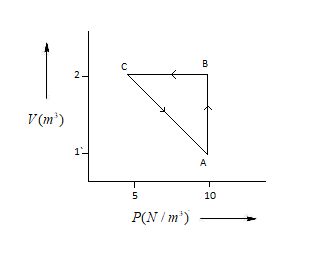
Here, ${{W}_{A\to C}}$=Work done in A to C
          ${{W}_{A\to B}}$=Work done in A to B
          ${{W}_{B\to C}}$= Work done in B to C

${{W}_{A\to B}}=P\Delta V=10(2-1)=10$.............(2)
Here, \[P\]=Pressure (Unit=\[N/{{m}^{3}}\])
            \[\Delta V\]= Volume (Unit=\[{{m}^{3}}\])

${{W}_{B\to C}}=P\Delta V=0$ .................(3)
 ($\because $$\Delta V=0$)

By putting value of equation (2) and (3) in equation (1) we get
${{W}_{A\to C}}=10+0-5$
$\therefore $ The work done by the gas in the process $C\to A$ is:
${{W}_{A\to C}}=5J$
Hence the correct option is (A)+5J.

-Since the temperature of the gas changes with its internal energy, it follows that adiabatic compression of a gas will cause it to warm up, while adiabatic expansion will result in cooling.

Note:
-If there is no change in temperature it means internal energy is Zero.
-In Adiabatic change the $q=0$ due to which the first law of thermodynamics is $\Delta U=0+W$.
-Observe the graph carefully to find the change in volume.