Question

An automobile moving at a speed of $72{\text{km}}{{\text{h}}^{ - 1}}$ reaches the foot of a smooth incline when the engine is switched off. Find the distance travelled by the automobile as it goes up the incline before stopping. The incline makes an angle $30^\circ $ with the horizontal. Take $g = 9.8{\text{m}}{{\text{s}}^{ - 2}}$ .

Answer 1

Hint: As the moving car reaches the foot of the incline it has kinetic energy, but once its moves along the incline after its engine gets switched off, the kinetic energy gets converted to potential energy. Thus according to the given information, as the automobile travels along the smooth incline before coming to rest, a transfer of energy takes place so that the change in the mechanical energy of the car is zero. The change in mechanical energy is the sum of the changes in potential energy and kinetic energy.

Formulae used:
The kinetic energy of a moving body is given by, $K.E = \dfrac{1}{2}m{v^2}$ where $m$ is the mass of the body and $v$ is its velocity.
The potential energy of a body at a height is given by, $P.E = mgh$ where $m$ is the mass of the body, $g$ is the acceleration due to gravity and $h$ is the height at which the body is placed.

Complete step by step answer:
Step 1: Sketch a figure depicting the problem at hand and list the known parameters.

In the figure, $h$ is the height from the horizontal at which the automobile comes to rest. $N$ is the normal force acting on the automobile and $W = mg$ is its weight where $m$ is the mass of the automobile
Let $s$ be the distance travelled by the automobile along the incline before coming to rest.
The initial velocity of the car is given to be $u = 72{\text{km}}{{\text{h}}^{ - 1}} = 72 \times \dfrac{5}{{18}} = 20{\text{m}}{{\text{s}}^{ - 1}}$ and its final velocity will be zero as it comes to rest i.e., $v = 0{\text{m}}{{\text{s}}^{ - 1}}$ .
The angle made by the incline with the horizontal is given to be $\theta = 30^\circ $ .
The acceleration due to gravity is given to be $g = 9.8{\text{m}}{{\text{s}}^{ - 2}}$ .
Step 2: Express the change in the kinetic energy and potential energy of the automobile for its motion.
The initial kinetic energy of the automobile can be expressed as $K.{E_i} = \dfrac{1}{2}m{u^2}$ ------ (1)
Substituting for $u = 20{\text{m}}{{\text{s}}^{ - 1}}$ in equation (1) we get the initial kinetic energy of the automobile as $K.{E_i} = \dfrac{1}{2}m \times {20^2} = 200m$
Now the final kinetic energy of the automobile will be zero as the car comes to rest i.e., $K.{E_f} = 0$ .
So the change in kinetic energy will $\Delta K.E = K.{E_f} - K.{E_i} = 0 - 200m = - 200m$ --------- (2)
Now the initial potential energy will be zero since initially, the car moves along the horizontal and the height is zero. So we have $P.{E_i} = 0$ .
The final potential energy once the automobile comes to rest is expressed as $P.{E_f} = mgh$.
Then the change in potential energy will be $\Delta P.E = P.{E_f} - P.{E_i} = mgh - 0 = mgh$ --------- (3)
Step 3: Express the change in the mechanical energy of the automobile for its motion to obtain the height $h$ and then the distance $s$ .
The change in the mechanical energy of the automobile for its motion will be zero.
i.e., $\Delta M.E = \Delta P.E + \Delta K.E = 0$
$ \Rightarrow \Delta P.E = - \Delta K.E$ --------- (4)
Substituting equations (2) and (3) in equation (4) we get, $mgh = - \left( { - 200m} \right) = 200m$
$ \Rightarrow h = \dfrac{{200}}{g}$
Now substituting for $g = 9.8{\text{m}}{{\text{s}}^{ - 2}}$ in the above expression we obtain the height as $h = \dfrac{{200}}{{9.8}} = 20.41{\text{m}}$
Now consider the below triangle whose sides are made up by the distance $s$ (hypotenuse), height $h$ and the horizontal as its base.

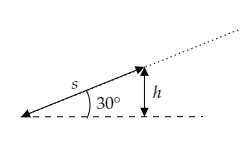
From the above-sketched figure, we have the distance travelled by the car to be $s = \dfrac{h}{{\sin \theta }} = \dfrac{{20.4}}{{\sin 30^\circ }} = 40.8{\text{m}}$
$\therefore $ the distance travelled by the automobile along the incline after its engine is switched off is obtained to be $s = 40.8{\text{m}}$ .

Note: Here the incline is said to be smooth, so frictional forces are not present. The absence of non-conservative forces leads to the conservation of the mechanical energy of the automobile. The work done by the normal reaction force is zero as the normal force and the displacement $s$ of the automobile are perpendicular to each other. The work done by the weight of the automobile is taken as the potential energy of the automobile.