Question

A uniform thin bar of mass 6 kg and length 2.4 meters is bent to make an equilateral hexagon. Find the moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the hexagon in terms of \[{10^{ - 1}}\,kg{m^2}\].

Answer 1

Hint:The moment of inertia is defined as the product of mass and the square of the distance from the axis of rotation of an object. It basically measures the rotational inertia of a body. This axis of rotation might be internal or external, and it can be fixed or not. But it is always described in relation to that axis.

Formula Used:
To find the moment of inertia passing through the centre of mass perpendicular to the plane is,
\[I = \left[ {\dfrac{{M{l^2}}}{{12}} + M{R^2}} \right]\]
Where, M is the mass, \[l\] is length and R is radius.

Complete step by step solution:

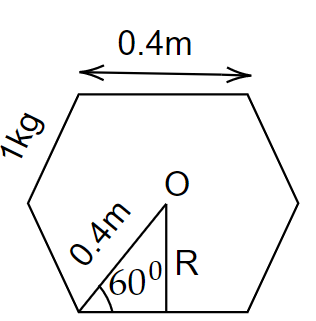
Image: An equilateral hexagon

Consider the uniform bar which is bent into an equilateral hexagon as shown in the figure. The mass of the uniform bar is 6kg, so the mass of each part is 1kg and the whole length is 2.4m, so the length of each part is 0.4m. We need to find the moment of inertia of the hexagon about an axis passing through the centre and perpendicular to the plane of the hexagon.

First, we will find the moment of inertia of a single part of this hexagon about an axis passing through its centre, then we use the parallel axis theorem and multiply by 6 which gives the total moment of inertia of the hexagon. Therefore, the moment of inertia of the hexagon is,
\[I = 6 \times \left[ {\dfrac{{M{l^2}}}{{12}} + M{R^2}} \right]\]……… (1)
From the diagram we have,
\[\sin {60^0} = \dfrac{R}{l}\]
\[\Rightarrow R = l\sin {60^0}\]
\[\Rightarrow R = \dfrac{{l\sqrt 3 }}{2}\]

Substitute the value of R in equation (1),
\[I = 6 \times \left[ {\dfrac{{M{l^2}}}{{12}} + M{{\left( {\dfrac{{l\sqrt 3 }}{2}} \right)}^2}} \right]\]
\[\Rightarrow I = 6 \times \left[ {\dfrac{{M{l^2}}}{{12}} + M{l^2}\left( {\dfrac{3}{4}} \right)} \right]\]
\[\Rightarrow I = 6 \times \left[ {\dfrac{{M{l^2} + 9M{l^2}}}{{12}}} \right]\]
\[\Rightarrow I = 6 \times \left[ {\dfrac{{10M{l^2}}}{{12}}} \right]\]
\[\Rightarrow I = 5M{l^2}\]

Substitute the value of \[M = 1kg\] and \[l = 0.4m\] in the above equation we get,
\[I = 5 \times 1 \times {\left( {0.4} \right)^2}\]
\[\Rightarrow I = 5 \times 0.16\]
\[\Rightarrow I = 0.8kg{m^2}\]
\[\therefore I = 8 \times {10^{ - 1}}kg{m^2}\]
Therefore, the moment of inertia of the hexagon is \[8 \times {10^{ - 1}}kg{m^2}\].

Hence, option A is the correct answer.

Note:In order to resolve this problem, we first need to find the value of R using the triangle as shown and then we need to find the moment of inertia about an axis passing through the centre of mass and also perpendicular to the plane of hexagon.