Question

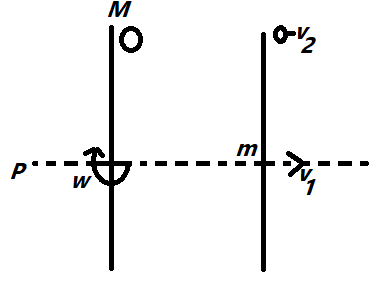
A uniform stick of mass m and length l with $I = \dfrac{1}{{12}}m{l^2}$ spins around on a frictionless horizontal plane, with its CM stationary A mass M is placed on the plane, and the stick collides elastically with it, as shown (with the contact point being the end of the stick) What should be the ratio of m/M be so that after the collision the stick has translational motion but no rotational motion?

Answer 1

Hint: Here in this question, we must know that , The body must be free to move in order to impart translational motion, and after applying force, all of the body's particles must move at the same speed. Therefore, in order for a force to rotate a body, it must travel via the rotational axis.

Formula Used:
Angular momentum,
$L = I\omega $
$e = \dfrac{\text{velocity of separation}}{\text{velocity of approach}}$

Complete step by step solution:
Here from above we get that, the angular momentum is,
$L = I\omega $
As according to the diagram, the stick is divided into two equal part of length $\dfrac{l}{2}$ hence the momentum will be,
$I\omega = M{v_2}\dfrac{l}{2}$
As we have the value of I in the question, by putting the value we get the resultant as,
$\dfrac{{m{l^2}}}{{12}}\omega = M{v_2}\dfrac{l}{2} .....(i)$
As by seeing for the linear momentum, there is no momentum there but after which the resultant momentum is,
$0 = m{v_1} + M{v_2} .....(ii)$

As this performs elastically also, so the value is,
$e = \dfrac{\text{velocity of separation}}{\text{velocity of approach}}$
As in mathematical view we can say it as,
$e = \dfrac{{{v_2} - {v_1}}}{{\omega \left( {\dfrac{l}{2}} \right)}} .....(iii)$
As this is elastic for which we know the value for it,
$M = \dfrac{m}{2}$
And according to question we need the ratio of m with M so, rearranging the equation as suitable,
$\dfrac{m}{M} = \dfrac{2}{1}$

Therefore, the correct answer for the ratio of masses is $2:1$.

Note:There is an important note for this question that, When two objects collide, there is no net loss of kinetic energy in the system. This is known as an elastic collision. In elastic collisions, kinetic energy and momentum are both conserved. A collision is considered to be inelastic if any of the kinetic energy is converted to another kind of energy during the collision.