
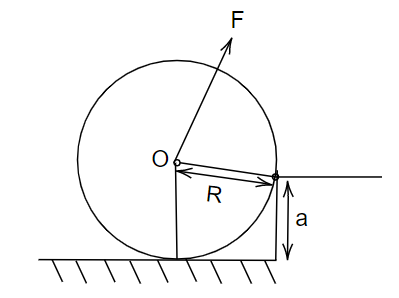
A uniform cylinder of mass M and radius R is to be pulled over a step of height \[\left( {a < R} \right)\]by applying a force F at its center ‘O’ perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). Then find the minimum value of F.
A. \[Mg\sqrt {{{\left( {\dfrac{R}{{R - a}}} \right)}^2} - 1} \]
B. \[Mg\sqrt {1 - \dfrac{{{a^2}}}{{{R^2}}}} \]
C. \[Mg\dfrac{a}{R}\]
D. \[Mg\sqrt {1 - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}} \]
Answer
219.6k+ views
Hint: Before we start addressing the problem, we need to know about the torque. It is a measure of the force that can cause an object to rotate about an axis and it is denoted by \[\tau \].
Formula Used:
To formula for torque is given by,
\[\tau = FR\]
Where, $F$ is force and $R$ is distance or radius.
Complete step by step solution:
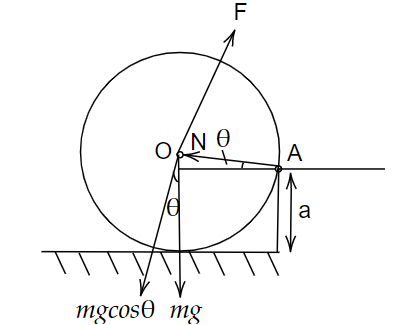
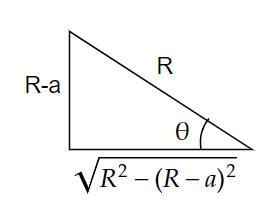
Consider a uniform cylinder of mass M and radius R is to be pulled over a step of height by applying a force F at its center ‘O’ perpendicular to the plane passing through the axes of the cylinder on the edge of the step. Then we need to find the minimum value of F.
In order to lift the sphere, if you see a point A, there should be a net torque about point A in the clockwise direction. There are two forces because of which the torque is coming. The two forces are F and mg. The torque because of F is \[{\tau _F} = FR\] in clockwise direction and \[{\tau _{mg}} = mgR\cos \theta \] in anticlockwise direction. Since, we want the toque in the clockwise direction. Therefore,
\[{\tau _F} \ge {\tau _{mg}}\]
\[\Rightarrow {\tau _F} \ge MgR\cos \theta \]
From the diagram we have,
\[\cos \theta = \dfrac{{\sqrt {{R^2} - {{\left( {R - a} \right)}^2}} }}{R}\]
\[ \Rightarrow \cos \theta = \sqrt {\dfrac{{{R^2}}}{{{R^2}}} - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}} \]
\[ \Rightarrow \cos \theta = \sqrt {1 - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}} \]
We want the minimum force, that is,
\[{F_{\min }} = mg\cos \theta \]
\[ \Rightarrow {F_{\min }} = mg\sqrt {1 - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}} \]
Therefore, the minimum value of force is, \[mg\sqrt {1 - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}}\].
Hence, option D is the correct answer.
Note:Here, the torque has both clockwise and anti-clockwise direction. Since the sphere is moving in the forward direction, we need to take the torque which is acting only in the clockwise direction. Some of the daily life examples of the torque are, opening the cap of a bottle or turning a steering wheel etc.
Formula Used:
To formula for torque is given by,
\[\tau = FR\]
Where, $F$ is force and $R$ is distance or radius.
Complete step by step solution:

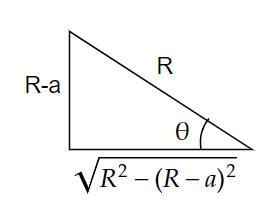
Consider a uniform cylinder of mass M and radius R is to be pulled over a step of height by applying a force F at its center ‘O’ perpendicular to the plane passing through the axes of the cylinder on the edge of the step. Then we need to find the minimum value of F.
In order to lift the sphere, if you see a point A, there should be a net torque about point A in the clockwise direction. There are two forces because of which the torque is coming. The two forces are F and mg. The torque because of F is \[{\tau _F} = FR\] in clockwise direction and \[{\tau _{mg}} = mgR\cos \theta \] in anticlockwise direction. Since, we want the toque in the clockwise direction. Therefore,
\[{\tau _F} \ge {\tau _{mg}}\]
\[\Rightarrow {\tau _F} \ge MgR\cos \theta \]
From the diagram we have,
\[\cos \theta = \dfrac{{\sqrt {{R^2} - {{\left( {R - a} \right)}^2}} }}{R}\]
\[ \Rightarrow \cos \theta = \sqrt {\dfrac{{{R^2}}}{{{R^2}}} - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}} \]
\[ \Rightarrow \cos \theta = \sqrt {1 - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}} \]
We want the minimum force, that is,
\[{F_{\min }} = mg\cos \theta \]
\[ \Rightarrow {F_{\min }} = mg\sqrt {1 - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}} \]
Therefore, the minimum value of force is, \[mg\sqrt {1 - {{\left( {\dfrac{{R - a}}{R}} \right)}^2}}\].
Hence, option D is the correct answer.
Note:Here, the torque has both clockwise and anti-clockwise direction. Since the sphere is moving in the forward direction, we need to take the torque which is acting only in the clockwise direction. Some of the daily life examples of the torque are, opening the cap of a bottle or turning a steering wheel etc.
Recently Updated Pages
Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

States of Matter Chapter For JEE Main Chemistry

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Atomic Structure for Beginners

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26




