Question

A taut string tension $100N$ and linear mass density $0.25kg/m$ is used inside a car to generate a wave pulse starting at the left end as shown. What should be the velocity of the cart so that the pulse remains stationary w.r.t. the ground?

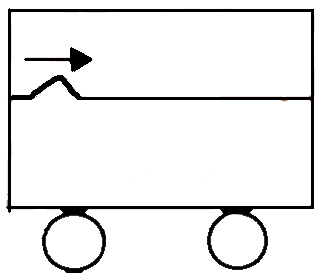
A) $-20i m/s$
B) $-30im/s$
C) $-40im/s$
D) $-50im/s$

Answer 1

Hint: In introduction to physics the pulses propagation on a taut string has always been an essential part. It illustrates uniform phase propagation, superposition and reflections which are concrete. It has more than obvious utility in string physics. Here, we need to find a relation between the tension in the string and the velocity. Put the given value and solve for the unknown.

Complete step by step solution:
The relationship between the tension and the velocity, it is given as:
\[S = \left( {\sqrt {\dfrac{T}{\mu }} } \right)\];
Here:
S = Velocity;
T = Tension;
\[\mu \]= Linear mass density;
Put the given value in the above equation:
\[S = \left( {\sqrt {\dfrac{T}{\mu }} } \right)\];
\[ \Rightarrow S = \left( {\sqrt {\dfrac{{100}}{{0.25}}} } \right)\];
Do, the necessary calculation:
\[ \Rightarrow S = \left( {\sqrt {\dfrac{{10000}}{{25}}} } \right)\];
\[ \Rightarrow S = \left( {\sqrt {400} } \right)\];
The value of the velocity is:
\[ \Rightarrow S = 20\]m/s;
$\overrightarrow {{V_P}} = \overrightarrow {{V_{PC}}} + \overrightarrow {{V_{CG}}} $;
Here:
$\overrightarrow {{V_P}} $= Velocity of pulse;
$\overrightarrow {{V_{PC}}} $= Velocity of pulse w.r.t. (relative) cart;
$\overrightarrow {{V_{CG}}} $= Velocity of cart w.r.t. (relative) ground;
$0 = 20 + \overrightarrow {{V_{CG}}} $;
$\overrightarrow {{V_{CG}}} = - 20i$;

Option (A) is correct. The velocity of the cart is -20i so that the pulse remains stationary w.r.t. the ground.

Note: Here the velocity of the cart should be opposite to the velocity of pulse w.r.t cart. Here, we need to see that the velocity of the cart is opposite as that is the only way to make the pulse look stationary while the pulse is moving in the positive direction.