Question

A sphere of radius ‘a’ and mass ‘m’ rolls along a horizontal plane with constant speed\[{v_0}\]. It encounters an inclined plane at angle \[\theta \] and climbs upward. Assuming that it rolls without slipping how far up the sphere will travel (along the incline)?

A. \[\dfrac{{\left( {\dfrac{2}{5}} \right){v_0}^2}}{{g\sin \theta }}\]
B. \[\dfrac{{10{v_0}^2}}{{7g\sin \theta }}\]
C. \[\dfrac{{{v_0}^2}}{{5g\sin \theta }}\]
D. \[\dfrac{{7{v_0}^2}}{{10g\sin \theta }}\]

Answer 1

Hint: Before we start addressing the question, we need to know about the inclined plane. It is a simple machine that consists of a sloping surface that is used for raising heavy bodies. If the incline plane’s angle keeps getting steeper, the force required also increases till it becomes equal to the weight of the object.

Formula Used:
From the conservation of energy, the formula is given by,
\[T{E_i} = T{E_f}\]
Where, \[T{E_i}\] is initial total energy and \[T{E_f}\] is final total energy.

Complete step by step solution:

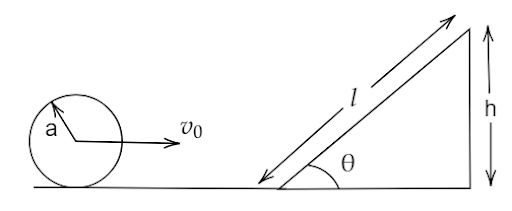
Consider a sphere of radius ‘a’ and mass ‘m’ rolls along the horizontal plane with constant speed (linear velocity)\[{v_0}\]. If the sphere is rolling without slipping then its angular velocity will be \[\omega \]and it reaches the inclined plane and starts climbing. We need to find how far the sphere will travel on an inclined plane.

In order to find that, we have
Initial total energy =final total energy
\[T{E_i} = T{E_f}\]
\[\Rightarrow K{E_{\left( {trans} \right)i}} + K{E_{\left( {rot} \right)i}} + P{E_i} = K{E_{\left( {trans} \right)f}} + K{E_{\left( {rot} \right)f}} + P{E_f}\]
We know that the total energy is equal to the sum of kinetic energy and potential energy.
\[\dfrac{1}{2}m{v_0}^2 + \dfrac{1}{2}I{\omega _0}^2 + 0 = 0 + 0 + mgh\]
\[\Rightarrow \dfrac{1}{2}m{v_0}^2 + \dfrac{1}{2}I{\omega _0}^2 = mgh\]
Since we know that, the moment of inertia is \[\dfrac{2}{5}m{a^2}\](radius \[r = a\]here) and by using the relation between linear and angular velocity,
\[\omega = \dfrac{v}{r}\]
\[ \Rightarrow \omega = \dfrac{v}{a}\].

Then the above equation will become,
\[\dfrac{1}{2}m{v_0}^2 + \dfrac{1}{2} \times \dfrac{2}{5}m{a^2}\dfrac{{{v_0}^2}}{{{a^2}}} = mgh\]
\[\Rightarrow \dfrac{1}{2}m{v_0}^2 + \dfrac{2}{{10}}m{v_0}^2 = mgh\]
\[\Rightarrow m\left( {\dfrac{1}{2}{v_0}^2 + \dfrac{1}{5}{v_0}^2} \right) = mgh\]
\[\Rightarrow gh = \dfrac{7}{{10}}{v_0}^2\]
\[\Rightarrow h = \dfrac{7}{{10g}}{v_0}^2\]

From the triangle,
\[\sin \theta = \dfrac{h}{l}\]
\[ \Rightarrow h = l\sin \theta \]
So, substitute the value in above equation we get,
\[l\sin \theta = \dfrac{7}{{10g}}{v_0}^2\]
\[ \therefore l = \dfrac{{7{v_0}^2}}{{10g\sin \theta }}\]
Therefore, the sphere will travel on an inclined plane at \[\dfrac{{7{v_0}^2}}{{10g\sin \theta }}\]

Hence, Option D is the correct answer.

Note:Remember that, if a sphere of some radius r is rolling with some speed v, then it has both translational and rotational motion. So, if we want to find the total energy then, it includes translational, rotational and also its potential energy.