Question

A sound source S is moving along a straight track with speed v, and is emitting the sound of frequency \[{v_0}\](see figure). An observer is standing at a finite distance, at the point o, from the track. The variation of frequency heard by the observer is best represented by (\[{t_0}\] represents the instant when the distance between the source and observer is minimum)
A.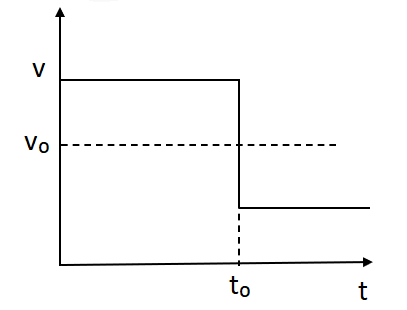
B.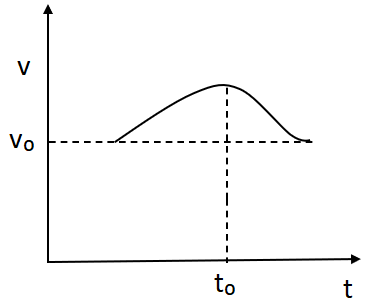
C.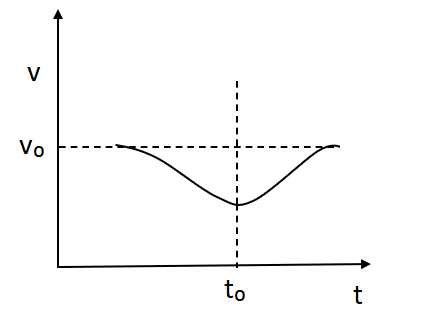
D.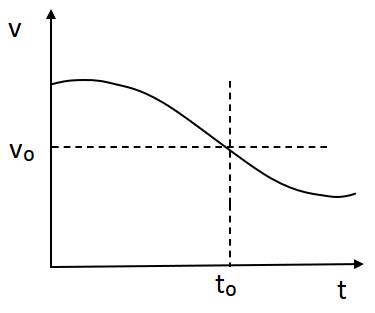

Answer 1

Hint: This question is related to the wave motion and the doppler effect. If a source is moving in a straight path with a velocity v and an observer is at some distance from the path. So, the source is coming to the observer. Hence the original frequency is \[{v_0}\].

Formula used:
\[{\upsilon ^1} = \dfrac{{{\upsilon _s}}}{{{\upsilon _s} - v\cos }}{\upsilon _0}\]
Where \[{\upsilon _s}\] is the frequency of the source and \[{\upsilon _0}\] is the frequency of the observer.

Complete step by step solution:
 In option B and C the initial frequency and final frequency is the same as the original frequency. The frequency heard by the observer in starting will be equal to the frequency that will be equal to the observer at rest. The relative velocity of the source towards the observer is equal to (\[ - v\cos \theta \]) where v is the sound velocity.
\[{\upsilon ^1} = \dfrac{{{\upsilon _s}}}{{{\upsilon _s} - v\cos {\upsilon _0}}}\]

From this relation, the variation of frequency is not linear. This depends on \[\cos \theta \]. So according to time. Here \[\theta \] will increase the value of \[\cos \theta \] and the value of frequency \[\upsilon '\] will decrease. Hence due to the variation of frequency with time, it is not linear it will depend on angle\[\theta \].

Hence option D is the correct answer.

Note: Now as we know that when the source is moving towards the observer then the frequency heard by the observer will be greater than the observer. So, the starting frequency is greater than the original frequency and after when it crosses that line the frequency will be less than the original frequency.