Question

A rolling body is kept on a plank B. There is sufficient friction between A and B and no friction between B and the inclined plane. Then body

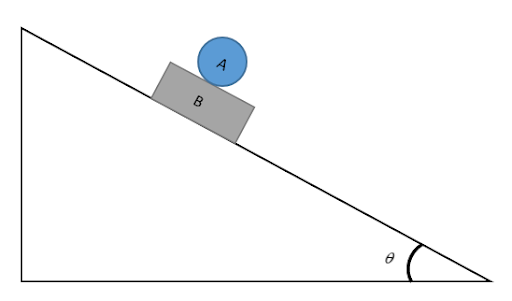
A. A Rolls
B. A doesn’t experience any friction
C. A and B have equal acceleration and unequal velocities.
D. A rolls depending upon the angle of inclination

Answer 1

Hint:when a body is moving under the influence on only gravitational force then the motion is said to be free fall. The body is at equilibrium along the direction perpendicular to the surface in contact.

Formula used:
\[{F_{net}} = ma\]
here \[{F_{net}}\] is the net force acting on the body of mass m and a is the acceleration produced.

Complete step by step solution:
As there is no friction between body B and the inclined surface, there will be no resistive force acting on it to oppose the motion. Using vector resolution for the weight of the plank B, we get the force on the plank B as,
\[{F_{B\parallel }} = {m_B}g\sin \theta \]
If acceleration of B on the inclined surface is \[{a_B}\] then using Newton’s 2nd law of motion,
\[{F_{B\parallel }} = m{a_B}\]
\[\Rightarrow {a_B} = \dfrac{{{m_B}g\sin \theta }}{{{m_B}}} = g\sin \theta \]

Similarly, for rolling sphere A, using vector resolution for the weight of the sphere A, we get the force on the sphere as,
\[{F_{A\parallel }} = m{a_A}\]
\[\Rightarrow {a_A} = \dfrac{{{m_A}g\sin \theta }}{{{m_A}}} = g\sin \theta \]
The magnitude of plank B and the sphere A along the inclined surface is same and also the direction is down the inclined surface. Hence, the relative acceleration of the sphere with respect to the plank is zero.

Using Newton’s 2nd law of motion,
\[{F_{net}} = ma\]
The force between the surfaces of the sphere and the plank is zero as the relative acceleration is zero. As we know that the frictional force is the resistive force which opposes the relative motion between the surfaces in contact, so there will be no friction between the surfaces of the sphere and the plank.

Therefore, the correct option is B.

Note: If the relative acceleration between the sphere and the plank was non-zero then frictional force will act on the sphere which will try to rotate the sphere and hence it may roll or slip based on the relative acceleration between A and B.