Question

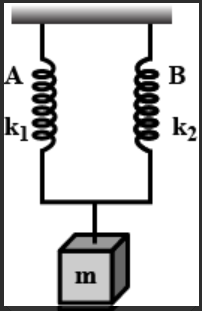
A mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constants are $k_1$​ and $k_2$​ respectively. When set into vertical vibrations, the period will be

A. $T = 2\pi \sqrt {\dfrac{m}{{{k_1}{k_2}}}} $
B. $T = 2\pi \sqrt {\dfrac{{m{k_1}}}{{{k_2}}}} $
C. $T = 2\pi \sqrt {\dfrac{m}{{{k_1} + {k_2}}}} $
D. $T = 2\pi \sqrt {\dfrac{m}{{{k_1} - {k_2}}}} $

Answer 1

Hint: We know that the spring constant is the minimum force which must be applied on the spring to disturb the equilibrium of the spring. This force then displaces the spring from its equilibrium position. Hooke's law gives the relationship between the displacements of the spring and the external force applied.

Formula used:
$F = - kx$and $f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} $

Complete answer:
We know that when an external force F is applied to a spring it produces a harmonic oscillation. The force applied on a spring produces a displacement x.

We also know from Hooke’s law that the magnitude of the force is directly proportional to the displacement of the spring. It is mathematically given as $F = - kx$ , k is the spring constant. It is also
the force applied on the spring to produce unit displacement. The negative sign indicates that the spring always resists the applied force.

Then the frequency f of the oscillation, when a body of mass m is attached to the spring, is given as
$f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} $

Here, there are two springs with spring constant $k_1$ and $k_2$. Also given that a mass m is suspended on them, and both the spring displace by the same length, say l, then the force due to the spring are given as
${F_1} = {k_1}l$ and ${F_2} = {k_1}l$

The force on m is given as $F = mg$
But $F = {F_1} + {F_2}$
$ \Rightarrow mg = {k_1}l + {k_2}l$
$ \Rightarrow mg = ({k_1} + {k_2})l$
Let $({k_1} + {k_2}) = k$
Then $mg = kl$

Then the time period of the oscillation is given as $T = 2\pi \sqrt {\dfrac{m}{k}} $
Put the value of $k = ({k_1} + {k_2})$
we get, $T = 2\pi \sqrt {\dfrac{m}{{{k_1} + {k_2}}}} $

Hence option C is correct.

Note: The force on the spring is either due to the compression or due to the extension of the spring. We can say that k is a restoring force which tries to restore the spring to its equilibrium position. The spring constant is expressed in terms of .