Question

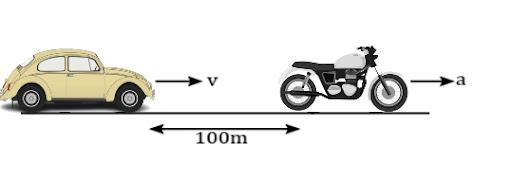
A man travelling in a car with a maximum constant speed of \[20\text{ }ms{{~}^{-1}}\] watches the friend start off at a distance 100 m ahead on a motorcycle with constant acceleration ‘a’. The maximum value of ‘a’ for which the man in the car can reach his friend is ?

A. $2\,m{{s}^{-1}}$
B. $1\,m{{s}^{-1}}$
C. $4\,m{{s}^{-1}}$
D. None of these

Answer 1

Hint:To do this question you have to know about Newton’s equation of motion. By applying the third equation of motion, we can solve this question. Here we have to find the maximum acceleration attained by the car to reach the bike. So, extreme conditions are also applied.

Formula used:
Here Newton's third equation of motion is used. Let a be the acceleration and u be the initial velocity and v be the final velocity and s be the distance travelled by the particle. Then, newton’s third equation of motion is:
${{v}^{2}}={{u}^{2}}+2as$

Complete step by step solution:
The car is travelling with a maximum constant speed of \[20\text{ }ms{{~}^{-1}}\]. Motorcycle which is 100 m away from the car is just starting and it is moving with constant acceleration. We have to find the acceleration attained by the car to reach the motorcycle.

If the man has to reach his friend, then his friend should not be faster than him until he covers the distance of 100 m. From the question it is clear that the initial velocity of the motorcycle is zero. That is, on applying Newton’s third equation of motion we get:
${{20}^{2}}\ge 200a$
That is,
$a<2$
From this condition we can say that the maximum acceleration of a car should be $2\,m{{s}^{-1}}$ to reach a motorcycle which is 100 m away from the car.

Hence, the correct answer is option A.

Note: If we know the basics, then this is a simple question. In this question without applying extreme conditions, we can find maximum acceleration attained by the car to reach the motor cycle which is 100 m away from the car.