Question

A light rod of length 2m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm² and the other of brass of cross-section 0.2cm². Along the rod at what distance a weight may be hung to produce equal stresses in both the wires? $\left( {{Y_{{\text{steel}}}} = 2 \times {{10}^{11}}{\text{ N}}{{\text{m}}^{ - 1}},{\text{ }}{{\text{Y}}_{{\text{brass}}}} = 1 \times {{10}^{11}}{\text{ N}}{{\text{m}}^{ - 2}}} \right)$.
(A) $\dfrac{4}{3}{\text{ m}}$ from steel wire.
(B) $\dfrac{4}{3}{\text{ m}}$ from brass wire.
(C) $1{\text{ m}}$ from steel wire.
(D) $\dfrac{1}{4}{\text{ m}}$ from brass wire.

Answer 1

Hint: Hint: Analyze the situation with a diagram. Use the formula, ${\text{Stress }} = \dfrac{{{\text{Force}}}}{{{\text{Cross Sectional Area}}}}$, to equalize the stress in both the wires and form and equation. Then frame an equation for rotational equilibrium by equalizing the torques. Solve these two equations simultaneously to find the required position.

Complete step by step answer:


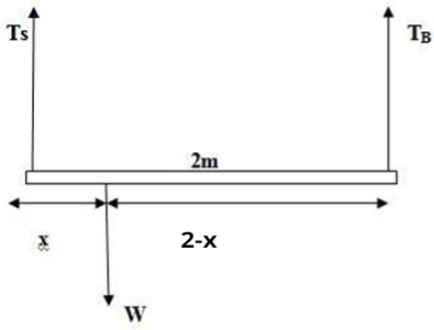
Consider the diagram of the suspended rod as shown above. On the left hand side it is tied with the steel wire carrying tension ${T_S}$ and on the right hand side it is tied with the brass wire carrying tension ${T_B}$.
Now, due to the tensions in the strings they will experience stress. We know that the stress in a solid can be calculated as:
$ \Rightarrow {\text{Stress }} = \dfrac{{{\text{Force}}}}{{{\text{Cross Sectional Area}}}}$
Further, the cross-sectional areas of steel and brass wires are given in the question as 0.1 cm² and 0.2 cm² respectively. And force experienced by the wires are the tensions ${T_S}$ and ${T_B}$.
So, applying the formula of stress, we’ll get:
$ \Rightarrow {\left( {{\text{Stress}}} \right)_{{\text{Steel}}}} = \dfrac{{{T_s}}}{{0.1{\text{ cm}}}}$ and ${\left( {{\text{Stress}}} \right)_{{\text{Brass}}}} = \dfrac{{{T_B}}}{{0.2{\text{ cm}}}}$
According to the question, we have to find the position in the rod where a weight can be hanged so as to achieve equal stress in both the wires.
So, the above two stresses must be equal for our condition to hold true. Thus we have:
$
   \Rightarrow \dfrac{{{T_s}}}{{0.1{\text{ cm}}}} = \dfrac{{{T_B}}}{{0.2{\text{ cm}}}} \\
   \Rightarrow \dfrac{{{T_S}}}{{{T_B}}} = \dfrac{{0.1}}{{0.2}} \\
   \Rightarrow \dfrac{{{T_S}}}{{{T_B}}} = \dfrac{1}{2}{\text{ }}.....{\text{(1)}} \\
$
Now let the weight hanged on the rod is at $x{\text{ m}}$ from the steel wire as shown in the figure. So its position from the brass wire will be $\left( {x - 2} \right){\text{ m}}$.
Considering this point as the point of rotation, the tension in the steel wire tends to rotate the rod in clockwise direction. So the torque experienced by the rod due to this tension force about the same point can be calculated using the formula:
$ \Rightarrow \tau = {\text{ Force}} \times {\text{Distance}}$
On putting values we’ll get:
$ \Rightarrow {\tau _{{\text{Steel}}}} = {T_S} \times x$
Similarly the torque produced by brass wire will tend to rotate the rod in anti-clockwise direction. Using the same torque formula, we’ll get:
$ \Rightarrow {\tau _{{\text{Brass}}}} = {T_B} \times \left( {2 - x} \right)$
For the rod to be in rotational equilibrium, both the rods must be equal. Thus we have:
\[ \Rightarrow {\tau _{{\text{Steel}}}} = {\tau _{{\text{Brass}}}}\]
Putting the values from above, we’ll get:
$
   \Rightarrow {T_S} \times x = {T_B} \times \left( {2 - x} \right) \\
   \Rightarrow \dfrac{{{T_S}}}{{{T_B}}} = \dfrac{{2 - x}}{x} \\
$
Putting the value of $\dfrac{{{T_S}}}{{{T_B}}}$ from the equation (1), we’ll get:
$
   \Rightarrow \dfrac{1}{2} = \dfrac{{2 - x}}{x} \\
   \Rightarrow x = 4 - 2x \\
   \Rightarrow 3x = 4 \\
   \Rightarrow x = \dfrac{4}{3}{\text{ m}} \\
$
Thus the position where the weight can be hanged is $\dfrac{4}{3}{\text{ m}}$ from steel wire. (A) is the correct option.

Note: This position will not be depended on the mass of the hanged weight unless the stresses in the wires do not exceed their breaking stresses. Also the values of Young’s Modulus of steel and brass given in the question are of no use to solve the question. The formula for Young’s Modulus is given as $Y = \dfrac{{{\text{Stress}}}}{{{\text{Strain}}}}$.But here we are not taking strain into consideration.